Структурные характеристики системы позволяют уже на ранней стадии создания системы оценить качество ее структуры и элементов с позиции общего системного подхода. Рассмотрим основные характеристики и приведем реализацию описанных алгоритмов анализа систем на языке программирования C#.
1 Связность структуры
1.1 Теоретические сведения
Эта характеристика позволяет выявить наличие обрывов в структуре, висячие вершины и т.п.
Связность элементов графа определяется матрицей связности С = ||cij||, элементы которой определяются на основе суммарной матрицы смежности:
где n – число вершин графа, Ak = Ak-1A (в частности A2 = A•A), где A – матрица смежности графа.
Элемент матрицы Ak = ||akij|| определяет число путей длиной k от вершины i к вершине j.
Элемент матрицы связности:
1.2 Программная реализация
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
public void connectionStructure(int n, int[,] A, int[,] C) { if (n > 0) { int[, ,] Ak = new int[n, n, n]; for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) Ak[0, i, j] = A[i, j]; for (int k = 1; k < n; k++) { for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) { Ak[k, i, j] = 0; for (int m = 0; m < n; m++) Ak[k, i, j] += Ak[k - 1, i, m] * A[m, j]; } } for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) C[i, j] = 0; for (int k = 0; k < n; k++) { for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) C[i, j] += Ak[k, i, j]; } for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) if (C[i, j] >= 1) C[i, j] = 1; } } |
Аргументы метода connectionStructure( ): n – число вершин в графе, A – матрица смежности, C – ссылка на экземпляр класса Array, в который будет занесена матрица связности.
2 Структурная избыточность
2.1 Теоретические сведения
Структурной избыточностью R называется параметр, отражающий превышение общего числа связей над минимально необходимым. R определяется следующим образом:
Для систем с избыточностью, имеющих кольцевую структуру или структуру типа «полный граф», R > 0, для систем без избыточности R = 0, для систем несвязных R < 0.
Обычно системы с большим R потенциально более надежны.
Для характеристики систем с большой избыточностью вводят также параметр ε2, учитывающий неравномерность распределения связей. При этом дуги у ориентированного графа рассматриваются без учета направленности.
где n – количество вершин, gi – степень i-ой вершины, m – количество ребер у графа.
Этот показатель характеризует недоиспользование возможностей структуры в достижении максимальной связности.
2.2 Программная реализация
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
public void structuralRedundancy(int n, int countE, int[,] A, out double R, out double e2) { R = 0; for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) R += A[i, j]; R = R * 0.5 / (double)(n - 1) - 1; e2 = 0; for (int i = 0; i < n; i++) { int degreeV = 0; for (int j = 0; j < n; j++) degreeV += A[i, j]; e2 += degreeV * degreeV; } e2 -= 4 * countE * countE / (double)n; } |
Аргументы метода structuralRedundancy( ): n – число вершин в графе, countE – количество ребер в графе, A – матрица смежности, R – структурная избыточность, e2 – неравномерность распределения связей. R и e2 – выходные параметры.
3 Структурная компактность
3.1 Теоретические сведения
Близость элементов i, j между собой определяется через минимальную длину цепи (пути) dij. Структурная компактность определяется несколькими параметрами.
Абсолютная компактность:
Относительная компактность:
где Qmin = n(n-1) – это минимальное значение компактности для структуры системы типа «полный граф»;
Диаметр структуры:
Чем выше эти параметры, тем инерционнее процессы, осуществляемые в системе, тем больше количество разделяющих элементы связей, тем меньше надежность.
3.2 Программная реализация
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
List<int> chainsLenght; public void structuralCompactness(int n, List<Edge> E, out int Q, out double Qotn, out int d) { chainsLenght = new List<int>(); Q = 0; d = 0; //1-white 2-black int[] color = new int[n]; for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) { if (i == j) continue; chainsLenght.Clear(); for (int k = 0; k < n; k++) color[k] = 1; DFSchain(i, j, E, color, 0); if (chainsLenght.Count > 0) { int min = chainsLenght[0]; foreach (int element in chainsLenght) { if (element < min) min = element; } Q += min; if (min > d) d = min; } } Qotn = (double)Q / (n * (n - 1)) - 1; } |
Аргументы метода structuralCompactness( ): n – число вершин в графе, E – список ребер графа, Q – абсолютная компактность, Qotn – относительная компактность, d – диаметр структуры. Q, Qotn и d – выходные параметры.
Ребро графа графа определяется экземпляром класс Edge:
|
1 2 3 4 5 6 7 8 9 10 |
class Edge { public int v1, v2; public Edge(int v1, int v2) { this.v1 = v1; this.v2 = v2; } } |
где v1 и v2 — номера вершин, которые соединяет данное ребро.
Для поиска длин цепей (заносятся в List<int> chainsLenght) в графе используется модификация рекурсивного алгоритма «Поиск в глубину» (Depth-first search). Опишем принцип ее работы:
Пусть дан граф G = (V, E), где V – множество вершин графа, E – множество его ребер. Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним следующие действия:
- Перебираем все пары вершин, возможно, они являются началом и концом цепи. На каждой итерации перекрашиваем все вершины в белый цвет (обозначим его 1, а черный цвет будем обозначать 2). Вызываем для каждой пары вершин процедуру DFSchain.
Процедура DFSchain(int u, int endV, List<Edge> E, int[] color, int len) (параметры: u – номер начальной вершины цепи, endV – номер конечной вершины цепи, E – список ребер графа, color — массив, в котором хранятся цвета вершин, len – текущая длина цепи):
- Если номер вершины u не равен endV, значит мы не достигли конца цепи, поэтому перекрашиваем вершину u в черный цвет. Иначе – конец цепи достигнут: добавляем длину цепи (len) в список и выполняем возврат из функции.
- Для всякой вершины w, смежной с вершиной u и окрашенной в белый цвет, рекурсивно выполняем процедуру DFSchain(w, endV, E, color, len + 1). Возвращаем вершине w белый цвет (возможно через нее проходят другие цепи, поэтому не будем исключать ее из рассмотрения).
Приведем реализацию метода DFSchain( ):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
private void DFSchain(int u, int endV, List<Edge> E, int[] color, int len) { //вершину не следует перекрашивать, если u == endV (возможно в нее есть несколько путей) if (u != endV) color[u] = 2; else { chainsLenght.Add(len); return; } for (int w = 0; w < E.Count; w++) { if (color[E[w].v2] == 1 && E[w].v1 == u) { DFSchain(E[w].v2, endV, E, color, len + 1); color[E[w].v2] = 1; } else if (color[E[w].v1] == 1 && E[w].v2 == u) { DFSchain(E[w].v1, endV, E, color, len + 1); color[E[w].v1] = 1; } } } |
4 Степень централизации в структуре
4.1 Теоретические сведения
Для оценки централизации используют индекс центральности:
где Zmax – максимальное значение величины:
Для структур систем, имеющих максимальную степень централизации σ = 1 (радиальная), для структур с равномерным распределением связей (полный граф, кольцевая) σ = 0.
4.2 Программная реализация
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
public double degreeOfCentralization(int n, int Q, List<Edge> E) { double[] Z = new double[n]; chainsLenght = new List<int>(); int[] color = new int[n]; for (int i = 0; i < n; i++) { int sumD = 0; for (int j = 0; j < n; j++) { if (i == j) continue; chainsLenght.Clear(); for (int k = 0; k < n; k++) color[k] = 1; DFSchain(i, j, E, color, 0); if (chainsLenght.Count > 0) { int min = chainsLenght[0]; foreach (int element in chainsLenght) { if (element < min) min = element; } sumD += min; } } Z[i] = (double)(Q / 2) / sumD; } double Zmax = Z[0]; foreach(double element in Z) { if (element > Zmax) Zmax = element; } double sigma; sigma = (double)(n - 1) * (2 * Zmax - n) / (Zmax * (n - 2)); return sigma; } |
Аргументы метода degreeOfCentralization( ): n – число вершин в графе, Q – значение абсолютной компактности, E – список ребер графа. Метод возвращает значение индекса централизации (sigma). Для поиска значений длины цепей между вершинами используется метод DFSchain( ), описанный выше.
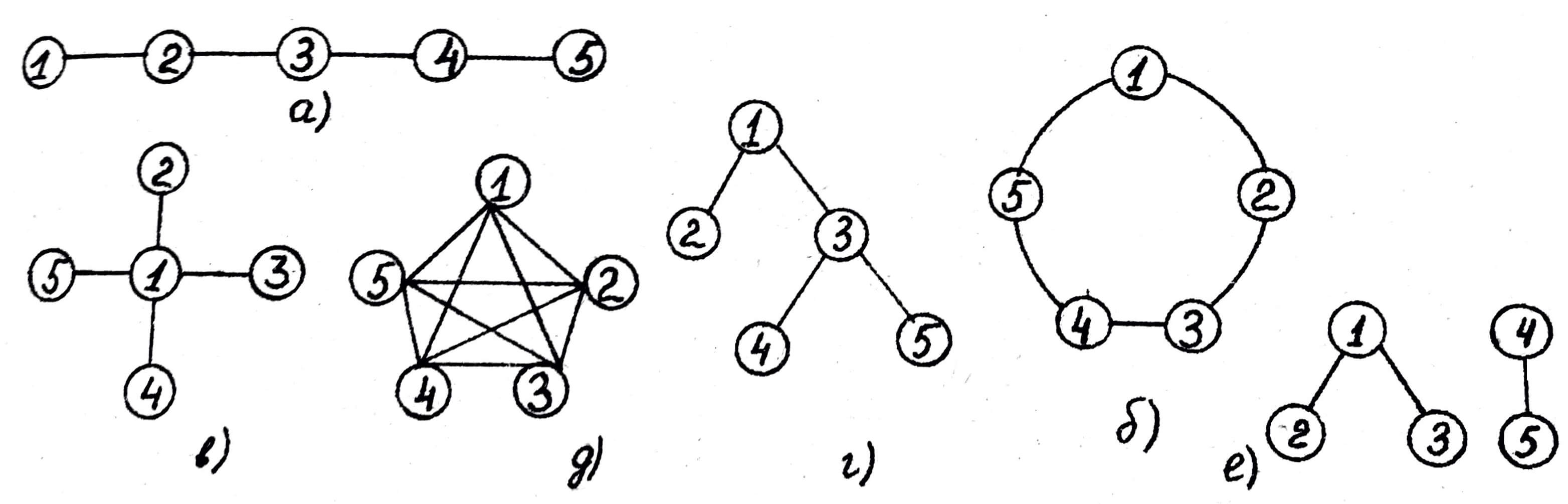
5 Основные виды структур
Введенные количественные характеристики могут быть использованы при сравнительной оценки топологических свойств структур систем. С точки зрения топологии внутренних связей выделяют следующие основные виды структур:
а) последовательная
б) кольцевая
в) радиальная
г) древовидная
д) типа «полный граф»
е) несвязная
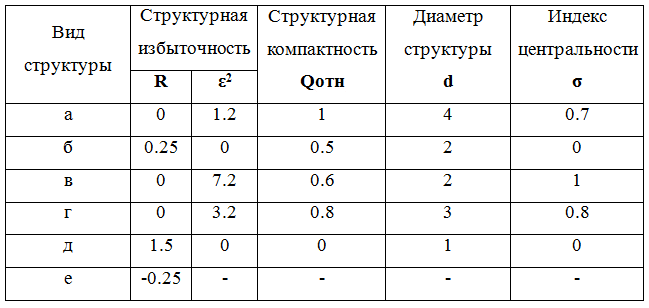
Количественные значения структурно-топологических характеристик этих структур приведены в таблице ниже.
Видно, что структуры с нулевой избыточностью R = 0 всё же различаются по параметру ε2. Наибольшую неравномерность связей имеет радиальная структура. Наибольшую компактность имеет структура типа «полный граф». Наименьшую близость элементов – последовательная структура. Структуры неразличимые по показателю d: кольцевая и радиальная – имеют различные значения параметра Q, т.е. кольцевая структура всё же более компактна, чем радиальная. Отметим также, что чем больше централизация, тем выше неравномерность связей (параметр ε2).
Скачать листинги
Поделиться в соц. сетях:
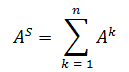
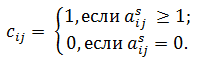
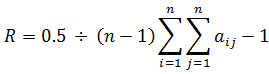
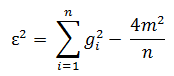
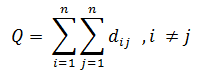
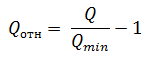
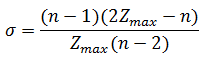
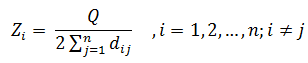
Никогда не видел понятие матрицы связности, но насколько я понимаю [latex]A^k[/latex] — это матрица достижимости. Если в клетке такой матрицы содержится единица, значит между элементами графа, соответствующими строке и столбцу существует путь длины не более k (в невзвешенном графе, по крайней мере).
Вы определяете матрицу связности как сумму матриц достижимости для всех k от 1 до n. Я не совсем понимаю что даст такая сумма. [latex]A^k[/latex] содержит информацию обо всех возможных путях в матрице — такая матрица позволит выявить компоненты связности и, в частности, изолированные вершины. А что в этом случае дает сумма?