В статье рассматривается система логического вывода с одной входной переменной. Приводятся теоретические сведения, алгоритмы, а также исходный код программы решающей данную задачу.
Система логического вывода. Некоторые определения
Нечеткой системой логического вывода с одной входной переменной называется совокупность из правил Ri, входной переменной A’ и выхода B’. Правила имеют вид:
R1: Если x есть A1, то y есть B1
R2: Если x есть A2, то y есть B2
…
Rn: Если x есть An, то y есть Bn
где Ai и Bi — это нечеткие множества из терм-множеств переменных x и y.
Выражение «x есть Ai» называют предпосылкой, а выражение «y есть Bi» называют следствием.
Вычисление выхода B’ возможно тремя способами с помощью, так называемых, правил. Рассмотрим эти правила логического вывода.
Первое правило логического вывода
Данный алгоритм основан на первоначальном вычислении индивидуальных выходов и их последующей агрегации. Шаги алгоритма:
1) Вычисление нечетких соответствий для каждого правила на основе импликации:
Ri = Ai → Bi, i = 1, …, n
2) Вычисление выходов для каждого правила с помощью композиции:
Bi‘ = A’ ∘ Ri, i = 1, …, n
3) Агрегация индивидуальных выходов:
B’ = Agg(B1, B2, …, Bn)
О видах импликации (→), композиции (∘), агрегации (Agg) и примерах их вычисления речь пойдет ниже.
Второе правило логического вывода
Это правило основано на первоначальной агрегации правил.
1) Вычисление нечетких соответствий для каждого правила на основе импликации:
Ri = Ai → Bi, i = 1, …, n
2) Агрегация правил:
R’ = Agg(R1, R2, …, Rn)
3) Вычисление выхода системы с помощью композиции:
B’ = A’ ∘ R’
Третье правило логического вывода
Вообще это правило используется для систем логического вывода с несколькими входными переменными, но существует его модификация для систем с одной входной переменной.
Алгоритм основан на вычислении уровня истинности предпосылки i-го правила. Уровень истинности это вещественное число, обозначается как αi. α вычисляется для каждого правила с помощью формулы:
αi = max min { A'(x), Ai(x) }
Шаги алгоритма:
1) Вычисление уровня истинности предпосылки для каждого правила:
αi, i = 1, …, n
2) Вычисление выходов для каждого правила с помощью импликации:
Bi‘ = αi → Bi, i = 1, …, n
3) Агрегация индивидуальных выходов:
B’ = Agg(B1‘, B2‘, …, Bn‘)
Виды импликации и их программная реализация
Есть два вида импликации: Импликация Мамдани и импликация Ларсена.
Импликация Мамдани находится по формуле:
R(x, y) = A(x) → B(y) = min { A(x), B(y) }
|
1 2 3 4 5 6 |
private void Mamdani(double[] A, double[] B, double[][] R) { for (int i = 0; i < A.Length; i++) for (int j = 0; j < B.Length; j++) R[i][j] = Min(A[i], B[j]); } |
То есть элементы матрицы R[A.Length][B.Length] заполняются за счет выбора минимального элемента из пары чисел взятых из нечетких множеств A и B.
Для лучшего понимания рассмотрим пример. Пусть есть нечеткое множество A = {100/0.4; 130/0.6; 160/0.8; 200/1} и нечеткое множество B = {400/0.5; 450/1; 500/0.5}. Вычислим с помощью импликации Мамдани значение R(A, B) = A → B.
Импликация Ларсена использует операцию умножения вместо операции минимума:
R(x, y) = A(x) → B(y) = A(x) * B(y)
|
1 2 3 4 5 6 |
private void Larsen(double[] A, double[] B, double[][] R) { for (int i = 0; i < A.Length; i++) for (int j = 0; j < B.Length; j++) R[i][j] = A[i] * B[j]; } |
Композиция
В качестве композиции используется max-min (максиминная) композиция. По существу максиминная композиция определяется как обычное произведение матриц, только вместо операции умножения вводится операция min, а вместо операции сложения – max.
B = A ∘ R можно вычислить с помощью метода:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
private void Max_Min(double[] A, double[][] R, double[] B) { List<double> tmpMAX = new List<double>(); for (int j = 0; j < R[0].GetLength(0); j++) { tmpMAX.Clear(); for (int k = 0; k < R.GetLength(0); k++) tmpMAX.Add(Min(A[k], R[k][j])); B[j] = tmpMAX.Max(); } } |
Агрегация при логическом выводе
Оператор max используют как оператор агрегации.
При агрегации индивидуальных выходов для каждой позиции степени уверенности выбирается максимальная величина степени уверенности для соответствующего элемента из всей совокупности индивидуальных выходов. Агрегация правил происходит аналогично. Из всей совокупности правил Ri для каждой позиции элемента в матрице выбирается максимальный, и таким образом строится матрица R’.
Система логического вывода с одной входной переменной. Реализация
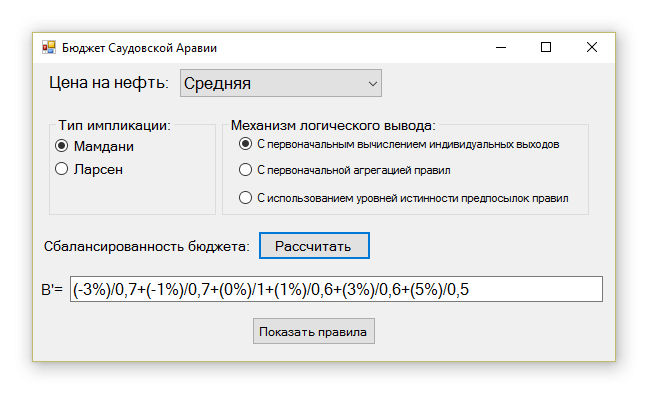
Приводим исходник программы, реализующей систему логического вывода с одной входной переменной. На рисунке представлен интерфейс программы.
Программа реализует логический вывод с помощью любого из трех правил (алгоритмов), описанных в данной статье. Кроме того, пользователь может выбрать тип импликации (Мамдани или Ларсена).
Скачать исходник
Опишем условие задачи, которую решает данная программа.
Задача. Зависимость сбалансированности бюджета Саудовской Аравии от цены на нефть.
Х = { 10$, 20$, 50$, 80$, 100$, 120$, 150$ } – множество определения Цена на нефть (в долларах США).
Y = { -3%, -1%, 0%, 1%, 3%, 5% } – множество определения Бюджет.
Цена на нефть:
Нечеткое множество Критически низкая
А = 10$/1 + 20$/0.8 + 50$/0.1 + 80$/0 + 100$/0 + 120$/0 + 150$/0
Нечеткое множество Очень низкая
А = 10$/1 + 20$/1 + 50$/0.3 + 80$/0 + 100$/0 + 120$/0 + 150$/0
Нечеткое множество Низкая
А = 10$/1 + 20$/1 + 50$/0.7 + 80$/0.2 + 100$/0 + 120$/0 + 150$/0
Нечеткое множество Приемлемая
А = 10$/0 + 20$/0.3 + 50$/0.9 + 80$/0.1 + 100$/0 + 120$/0 + 150$/0
Нечеткое множество Ниже среднего
А = 10$/0 + 20$/0.4 + 50$/0.8 + 80$/0.2 + 100$/0 + 120$/0 + 150$/0
Нечеткое множество Средняя
А = 10$/0 + 20$/0.1 + 50$/0.7 + 80$/1 + 100$/0.5 + 120$/0 + 150$/0
Нечеткое множество Выше среднего
А = 10$/0 + 20$/0 + 50$/0.2 + 80$/0.6 + 100$/0.9 + 120$/0.1 + 150$/0
Нечеткое множество Высокая
А = 10$/0 + 20$/0 + 50$/0.1 + 80$/0.4 + 100$/0.6 + 120$/0.6 + 150$/0.1
Нечеткое множество Очень высокая
А = 10$/0 + 20$/0 + 50$/0 + 80$/0.2 + 100$/0.5 + 120$/0.9 + 150$/0.5
Нечеткое множество Неимоверно высокая
А = 10$/0 + 20$/0 + 50$/0 + 80$/0.1 + 100$/0.3 + 120$/0.8 + 150$/1
Бюджет:
Нечеткое множество Очень дефицитный
В = (-3%)/1 + (-1%)/0.7 + (0%)/0 + (1%)/0 + (3%)/0 + (5%)/0
Нечеткое множество Дефицитный
В = (-3%)/0.8 + (-1%)/1 + (0%)/0.1 + (1%)/0 + (3%)/0 + (5%)/0
Нечеткое множество Сбалансированный
В = (-3%)/0 + (-1%)/0.5 + (0%)/1 + (1%)/0.5 + (3%)/0 + (5%)/0
Нечеткое множество Профицитный
В = (-3%)/0 + (-1%)/0 + (0%)/0.1 + (1%)/0.9 + (3%)/0.9 + (5%)/0.3
Нечеткое множество Очень профицитный
В = (-3%)/0 + (-1%)/0 + (0%)/0 + (1%)/0.2 + (3%)/0.7 + (5%)/1
Правила:
Если Цена на нефть Критически низкая, то Бюджет Очень дефицитный
Если Цена на нефть Очень низкая, то Бюджет Очень дефицитный
Если Цена на нефть Низкая, то Бюджет Дефицитный
Если Цена на нефть Приемлемая, то Бюджет Дефицитный
Если Цена на нефть Ниже среднего, то Бюджет Сбалансированный
Если Цена на нефть Средняя, то Бюджет Сбалансированный
Если Цена на нефть Выше среднего, то Бюджет Профицитный
Если Цена на нефть Высокая, то Бюджет Профицитный
Если Цена на нефть Очень высокая, то Бюджет Очень профицитный
Если Цена на нефть Неимоверно высокая, то Бюджет Очень профицитный
На вход подается нечеткое множество из множества определений Цена на нефть.
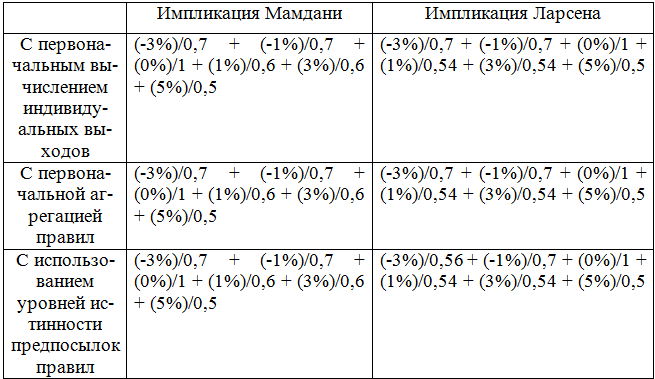
Сравним результаты вычислений, полученные с помощью разных механизмов логического вывода.
Пусть на вход подается Цена на нефть – Средняя:
А’ = 10$/0 + 20$/0.1 + 50$/0.7 + 80$/1 + 100$/0.5 + 120$/0 + 150$/0, тогда
Результаты, полученные с помощью разных механизмов логического вывода, получились одинаковые.
Результаты, полученные с помощью разных видов импликации, отличаются незначительно. Причем значения, полученные с помощью импликации Ларсена, оказались ниже.
Скачать исходник
Литература по теме:
1) Блюмин С.Л., Шуйкова И.А., Сараев П.В., Черпаков И.В. Нечеткая логика: алгебраические основы и приложения. Липецк: ЛЭГИ, 2002 – 107с.
Поделиться в соц. сетях: