Рассмотрим алгоритм Прима. Он используется для построения минимального остовного дерева на связном неориентированном графе. Будет приведено описание алгоритма и его реализация на языке программирования C#.
Алгоритм Прима — это алгоритм поиска минимального остовного дерева связного взвешенного неориентированного графа. Был открыт Робертом Примом в 1957 году.
Вес ребра — числовое значение, поставленное в соответствие данному ребру графа. Вес ребра можно интерпретировать как длину ребра.
Взвешенный граф — граф, для каждого ребра которого задан вес.
Связный граф — это такой граф, в котором из любой его вершины можно попасть в любую другую вершину.
Остовное дерево — это связный подграф без циклов данного связного неориентированного графа, в который входят все его вершины. Минимальное остовное дерево — это остовное дерево данного графа имеющее минимальный возможный вес. Под весом остовного дерева понимается сумма весов всех ребер, входящих в него.
Описание алгоритма Прима
На входе имеется взвешенный связный неориентированный граф.
Выбирается произвольная вершина данного графа и находится ребро, инцидентное данной вершине и обладающее наименьшим весом. Найденное ребро и две соединяемые им вершины образуют дерево. Затем рассматриваются ребра графа: один конец которых — это вершина, входящая в дерево, а другой — нет. Из набора этих ребер выбирается ребро с наименьшим весом. Найденное на каждом шаге ребро присоединяется к дереву. Следовательно, на каждом шаге алгоритма, высота формируемого дерева увеличивается на единицу. Работа алгоритма продолжается до тех пор, пока в дерево не будут включены все вершины данного графа.
На выходе имеем минимальное остовное дерево.
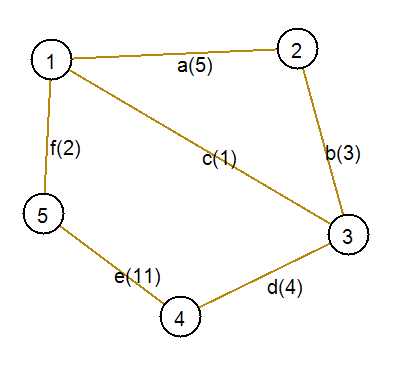
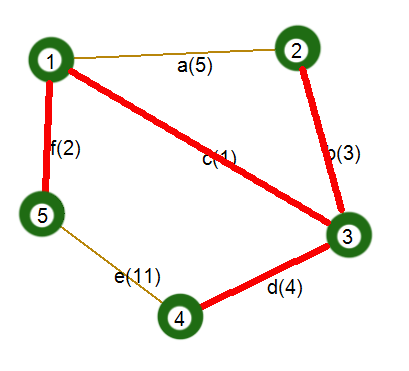
Приведем пример работы алгоритма. Пусть дан граф, как на рисунке ниже. В скобках указаны веса ребер.
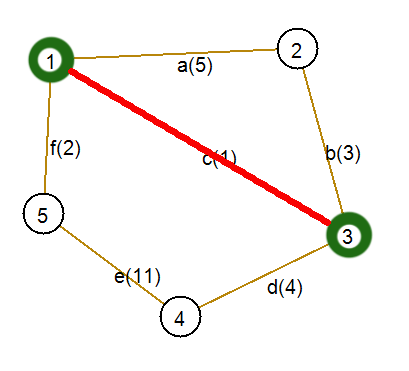
Шаг 1. Выберем произвольную вершину. Пусть это будет вершина номер 3. Ей инцидентны ребра (с неиспользованными вершинами): b(3), c(1), d(4). Ребро с наименьшим весом — c. Включим его и инцидентную ему вершину в дерево.
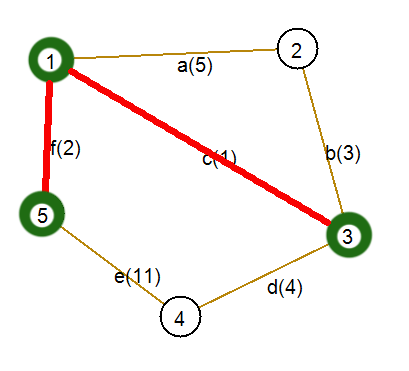
Шаг 2. Вершинам 1 и 3 инцидентны ребра (с неиспользованными вершинами): a(5), b(3), d(4), f(2). Ребро с наименьшим весом — f. Включим его и инцидентную ему вершину в дерево.
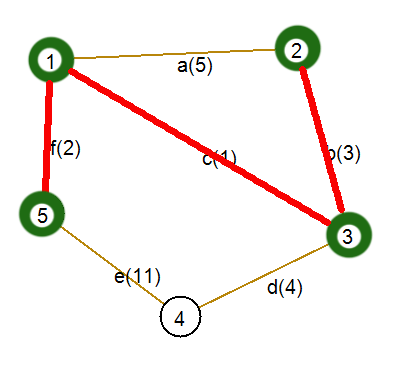
Шаг 3. Вершинам 1, 3 и 5 инцидентны ребра (с неиспользованными вершинами): a(5), b(3), d(4), e(11). Ребро с наименьшим весом — b. Включим его и инцидентную ему вершину в дерево.
Шаг 4. Вершинам 1, 2, 3 и 5 инцидентны ребра (с неиспользованными вершинами): d(4) и e(11). Ребро с наименьшим весом — d. Включим его и инцидентную ему вершину в дерево.
Все вершины графа включены в дерево. Работа алгоритма завершена.
Реализация алгоритма
Пусть ребро графа представлено экземпляром класса Edge:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
class Edge { public int v1, v2; public int weight; public Edge(int v1, int v2, int weight) { this.v1 = v1; this.v2 = v2; this.weight = weight; } } |
, где v1 и v2 — номера вершин (нумерация вершин начинается с нуля), инцидентных ребру, а weight — вес ребра.
А все ребра графа пусть представлены в виде списка:
|
1 |
List<Edge> E; |
Приведем реализацию алгоритма Прима на языке C#.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
public void algorithmByPrim(int numberV, List<Edge> E, List<Edge> MST) { //неиспользованные ребра List<Edge> notUsedE = new List<Edge>(E); //использованные вершины List<int> usedV = new List<int>(); //неиспользованные вершины List<int> notUsedV = new List<int>(); for (int i = 0; i < numberV; i++) notUsedV.Add(i); //выбираем случайную начальную вершину Random rand = new Random(); usedV.Add(rand.Next(0, numberV)); notUsedV.RemoveAt(usedV[0]); while (notUsedV.Count > 0) { int minE = -1; //номер наименьшего ребра //поиск наименьшего ребра for (int i = 0; i < notUsedE.Count; i++) { if ((usedV.IndexOf(notUsedE[i].v1) != -1) && (notUsedV.IndexOf(notUsedE[i].v2) != -1) || (usedV.IndexOf(notUsedE[i].v2) != -1) && (notUsedV.IndexOf(notUsedE[i].v1) != -1)) { if (minE != -1) { if (notUsedE[i].weight < notUsedE[minE].weight) minE = i; } else minE = i; } } //заносим новую вершину в список использованных и удаляем ее из списка неиспользованных if (usedV.IndexOf(notUsedE[minE].v1) != -1) { usedV.Add(notUsedE[minE].v2); notUsedV.Remove(notUsedE[minE].v2); } else { usedV.Add(notUsedE[minE].v1); notUsedV.Remove(notUsedE[minE].v1); } //заносим новое ребро в дерево и удаляем его из списка неиспользованных MST.Add(notUsedE[minE]); notUsedE.RemoveAt(minE); } } |
Аргументы метода algorithmByPrim: numberV — количество вершин в исходном графе, E — список ребер исходного графа, MST — список, в который будут занесены ребра, составляющие минимальное остовное дерево.
Кратко опишем работу метода algorithmByPrim(). В начале инициализируются списки с данными: ребра, не включенные в дерево, вершины, включенные в дерево, и вершины, не включенные в дерево (строки 4-10). Затем выбирается случайная начальная вершина, с которой начнется построение минимального остовного дерева (строки 12-14). Цикл while будет продолжаться до тех пор, пока все вершины графа не будут включены в дерево (15-47). На каждой итерации цикла выполняется следующее:
- Производится поиск ребра с наименьшим весом, один конец которого — это вершина, входящая в дерево, а другой — нет (строки 19-32).
- Вершина, инцидентная найденному ребру, заносится в список использованных и удаляется из списка неиспользованных (строки 34-43).
- Найденное ребро заносится в список ребер, составляющих дерево, и удаляется из списка неиспользованных ребер (строки 45-46).
Перед вызовом метода algorithmByPrim(), необходимо создать список, в котором будут хранится ребра, составляющие минимальное остовное дерево:
|
1 2 |
List<Edge> MST = new List<Edge>(); algorithmByPrim(V.Count, E, MST); |
Поделиться в соц. сетях:
Здравствуйте! спасибо, есть готовая программа на c# ?
Здравствуйте! Да, есть готовая программа, реализующая алгоритм Прима на C#, Windows Forms.
Можем предоставить видео с демонстрацией программы. Если Вас программа устроит, то можете ее купить. 200р.
А можно тоже готовую программу?
Ответили Вам на почту.
А можно и мне тоже готовую программу, спасибо.