В этой статье рассматривается симплекс-метод, который применяется при решении задач линейного программирования (ЗЛП). Приводится алгоритм метода, а также его реализация на языке C#. Реализация представлена в конце статьи.
Определения
Симплекс-метод — это алгоритм, используемый при решении оптимизационной задачи линейного программирования.
Линейное программирование — это раздел математики, занимающийся решением экстремальных задач (нахождением экстремума функции) на множестве пространства, заданном системой линейных уравнений и неравенств.
Оптимизация — задача нахождения минимума или максимума (экстремума) целевой функции.
Целевая функция — это функция нескольких переменных, подлежащая оптимизации в целях решения какой-либо оптимизационной задачи (например, задачи объемного планирования).
Алгоритм симплекс-метода
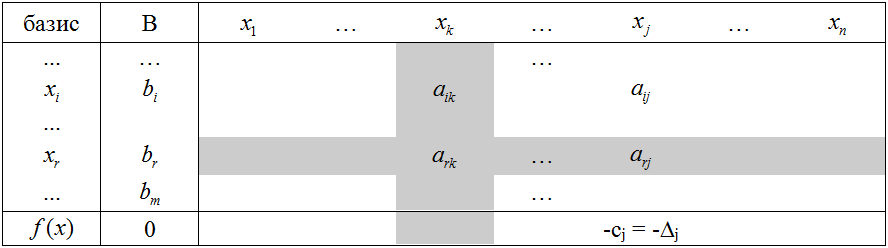
В начале исходную задачу линейного программирования приводят к каноническому виду, затем составляют симплекс-таблицу вида:
где в столбце «базис» указываются базисные переменные, а в последней строке столбца «базис» пишется f(x). В столбец «B» записываются свободные члены ограничений bi и значение целевой функции (на 1-м этапе оно равно 0, т.е. никакой прибыли).
В столбцах xj для не базисных переменных указываются коэффициенты при не базисных переменных из ограничений задачи. В столбцах базисных переменных содержится только 0 или 1 на пересечении столбца с соответствующей строкой базисной переменной.
В последней строке -cj — это коэффициенты при переменных целевой функции взятые с противоположным знаком.
Симплекс-таблица составлена, теперь опишем сам симплекс-метод.
Шаг 1: Выполняется проверка полученного базисного плана на оптимальность по условию: если при каком-либо ДБР (допустимое базисное решение) в симплекс-таблице все коэффициенты строки f(x) (то есть -cj) не отрицательны, то данное ДБР оптимально, следовательно КОНЕЦ решения. В противном случае:
Шаг 2: Переход к новому базисному плану. Для этого из числа небазисных переменных с отрицательными значениями в последней строке (то есть -cj < 0) выбирается переменная, вводимая в базис — xk, это переменная которой соответствует наибольшая по модулю отрицательная оценка:
Столбец, отвечающий переменной xk, называется главным, или ведущим. Элементы данного столбца обозначаются через aik.
Если окажется несколько одинаковых наибольших по модулю отрицательных оценок, то выбирается любая из соответственных переменных.
Шаг 3: Выбираем переменную r — переменную, которая выводится из базиса. Данная переменная находится из соотношения:
Строка таблицы, в которой получено наименьшее отношение элемента столбца «В» к соответствующему положительному элементу ведущего столбца, является ведущей, или главной.
Элементы главной строки обозначаются через arj. Выбранная переменная xr будет выводиться из базиса, то есть это исключаемая переменная.
Если окажется несколько одинаковых наименьших значений отношений, то выбирается любая из соответствующих им переменных.
Элемент, который стоит на пересечении главного столбца и строки называется главным, или ведущим, и обозначается ark.
Шаг 4: Для определения нового базисного плана проводится пересчет элементов симплекс-таблицы, и результаты заносятся в новую таблицу. Выбранные переменные среди базисных и не базисных, лежащих на главной строке и главном столбце, меняются местами.
Процедура пересчета элементов выполняется следующим образом:
а) элементы главной строки необходимо разделить на ведущий элемент:
б) элементы полученной строки умножаются на -aik, и результаты складываются с i-той строкой, причем i ≠ k:
После определения новой симплекс-таблицы переходят к шагу 1.
Симплекс-метод. Реализация C#
Приводим программную реализацию симплекс-метода. Программа написана на языке программирования C#.
Важная информация! Пожалуйста прочтите!
Входные данные: симплекс-таблица без базисных переменных в столбцах. То есть таблица должна быть построена только по коэффициентам при переменных из ограничений задачи и целевой функции.
Формат входных данных: двумерный массив из элементов типа double.
Входные данные передаются в качестве аргумента, при создании экземпляра класса Simplex.
При вызове метода Calculate в качестве аргумента вы должны передать одномерный массив из элементов типа double, длиной в количество переменных в целевой функции. В этот массив будут записаны найденные значения неизвестных.
Выходные данные: метод Calculate возвращает ссылку на двумерный массив, содержащий решенную симплекс-таблицу. Кроме того решение будет занесено в массив, переданный в качестве аргумента в метод Calculate.
Формат выходных данных: двумерный массив из элементов типа double и одномерный массив из элементов типа double.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Simplex { public class Simplex { //source - симплекс таблица без базисных переменных double[,] table; //симплекс таблица int m, n; List<int> basis; //список базисных переменных public Simplex(double[,] source) { m =source.GetLength(0); n = source.GetLength(1); table = new double[m, n + m - 1]; basis = new List<int>(); for (int i = 0; i < m; i++) { for (int j = 0; j < table.GetLength(1); j++) { if (j < n) table[i, j] = source[i, j]; else table[i, j] = 0; } //выставляем коэффициент 1 перед базисной переменной в строке if ((n + i) < table.GetLength(1)) { table[i, n + i] = 1; basis.Add(n + i); } } n = table.GetLength(1); } //result - в этот массив будут записаны полученные значения X public double[,] Calculate(double[] result) { int mainCol, mainRow; //ведущие столбец и строка while (!IsItEnd()) { mainCol = findMainCol(); mainRow = findMainRow(mainCol); basis[mainRow] = mainCol; double[,] new_table = new double[m, n]; for (int j = 0; j < n; j++) new_table[mainRow, j] = table[mainRow, j] / table[mainRow, mainCol]; for (int i = 0; i < m; i++) { if (i == mainRow) continue; for (int j = 0; j < n; j++) new_table[i, j] = table[i, j] - table[i, mainCol] * new_table[mainRow, j]; } table = new_table; } //заносим в result найденные значения X for (int i = 0; i < result.Length; i++) { int k = basis.IndexOf(i + 1); if (k != -1) result[i] = table[k, 0]; else result[i] = 0; } return table; } private bool IsItEnd() { bool flag = true; for (int j = 1; j < n; j++) { if (table[m - 1, j] < 0) { flag = false; break; } } return flag; } private int findMainCol() { int mainCol = 1; for (int j = 2; j < n; j++) if (table[m - 1, j] < table[m - 1, mainCol]) mainCol = j; return mainCol; } private int findMainRow(int mainCol) { int mainRow = 0; for (int i = 0; i < m - 1; i++) if (table[i, mainCol] > 0) { mainRow = i; break; } for (int i = mainRow + 1; i < m - 1; i++) if ((table[i, mainCol] > 0) && ((table[i, 0] / table[i, mainCol]) < (table[mainRow, 0] / table[mainRow, mainCol]))) mainRow = i; return mainRow; } } } |
Скачать файл Simplex.cs
Приведем также пример программы, использующей реализованный выше симплекс-метод. Решим, для примера, задачу с такими ограничениями и целевой функцией:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace testSimplex { class Program { static void Main(string[] args) { double[,] table = { {25, -3, 5}, {30, -2, 5}, {10, 1, 0}, { 6, 3, -8}, { 0, -6, -5} }; double[] result = new double[2]; double[,] table_result; Simplex S = new Simplex(table); table_result = S.Calculate(result); Console.WriteLine("Решенная симплекс-таблица:"); for (int i = 0; i < table_result.GetLength(0); i++) { for (int j = 0; j < table_result.GetLength(1); j++) Console.Write(table_result[i, j] + " "); Console.WriteLine(); } Console.WriteLine(); Console.WriteLine("Решение:"); Console.WriteLine("X[1] = " + result[0]); Console.WriteLine("X[2] = " + result[1]); Console.ReadLine(); } } } |
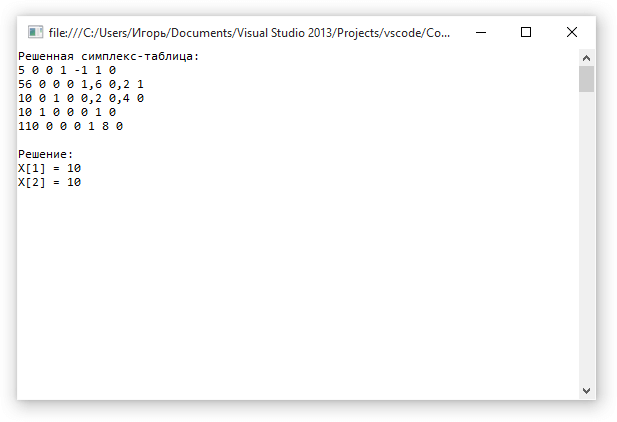
Демонстрация работы симплекс-метода:
Поделиться в соц. сетях:
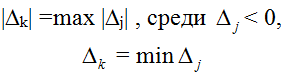
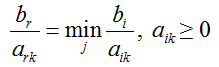
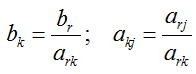
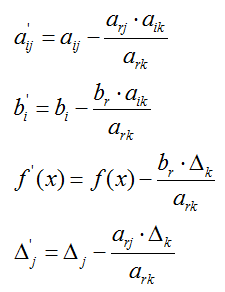
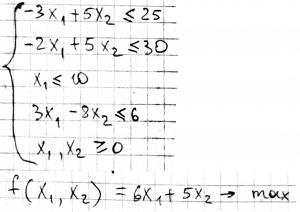
Спасибо, очень полезная информация и программа!
А что нужно сделать, чтобы функции искали переменные для минимума, а не для максимума?
Нужно поменять знак у функции: min(f(x)) = max(-f(x))
то есть сменить знаки коэффициентов при переменных? если так, то программа всё равно считает максимум
Да. Странно, должно было сработать.
получается здесь не учитывается знак ограничения? и прога только для <=?
Перед вводом данных в программу задачу нужно привести к каноническому виду.
Что вы подразумеваете под привести задачу к каноническому виду? Канонический вид, это же вроде:
1)инвертировать знаки у ф-ции F
2)добавить доп.переменные, 1 если знак неравенства =, это канонический вид.
У вас же таблица на входе имеет вид —-B—X1—X2 или я что-то не понимаю? Скажите пожалуйста, как именно нужно обработать систему неравенств?
Задача приводится к каноническому виду так, чтобы в системе ограничений знаки стали равенствами.
А в программу заносятся коэффициенты из приведённых ограничений:
b1 a11 a12 …
b2 a21 a22 …
…
0 -c1 -c2 …
При этом коэффициенты при базисных переменных (тех, которые вы добавляли, чтобы в ограничениях сделать равенства) НЕ нужно давать на вход программе!
Доброго времени суток. Скажите, а как, например, после решения задачи в добавок к выводу переменных сделать еще вывод значения целевой функции?
Перед вычислениями сохраните в отдельный массив значения коэффициентов при иксах: например в массив a.
После того, как массив result будет получен, найдём значение целевой функции F:
double F = 0;
for(int i = 0; i < result.Length; i++) { F += a[i] * result[i]; }
Спасибо за ответ! Скажите, а как всё-же сделать так, чтобы выполнялось составление симплексной таблицы для решения задачи на определение минимального плана?
Есть два пути.
1) Самый простой: привести задачу минимизации (сами исходные данные) к задаче максимизации и использовать приведённый выше алгоритм. Как преобразовать написано здесь.
2) Изменить приведённый алгоритм конкретно под задачу минимизации. При минимизации целевой функции ведущий столбец определяется по наибольшему значению в строке индексов. Читать про это подробнее.
Админ, спасибо за реализацию, а какой будет алгоритм, если мне необходимо в одной задачи использовать ограничения ‘=>’ и ‘<=' Можете посоветовать русскую литературу по симплекс методу.
Алгоритм будет точно такой же. Ведь система неравенств всё равно приводится к каноническому виду (в системе ограничений знаки становятся равенствами).
В предыдущем моём комментарии есть ссылка, там как раз есть пример с разными знаками в системе неравенств.
admin, помогите, пожалуйста, разобраться с вводом данных моей задачи. Заранее извиняюсь за столь глупый вопрос.
Ограничения:
2*y1+5*y2=1
6*y1+1*y2=1
Функция:
1*y1+1*y2 —> max
Здравствуйте! Вот такие данные будут у Вас:
1 2 5
1 6 1
0 -1 -1
Будет ли программа работать для более, чем двух переменных? Что нужно менять в коде, кроме входной матрицы?
Будет. В коде ничего менять не нужно.
Спасибо вам огромнейшее!
Здравствуйте. Простите за глупый вопрос, а как запустить эту программу?
Здравствуйте! Нужно создать проект консольного приложения на C#, например, в Visual Studio, добавить в проект класс Simplex (из данной статьи) и код в классе Program заменить на тот, что представлен в статье.
Сделал так, как и описали. Но в 21 строке 13 и 29 столбцы помешает как ошибку : simplex является «пространство имен» но используется как «тип». Не подскажете в чем причина может быть?
Изменили в файле с классом Simplex название пространства имен «Simplex» на то, которое у вас в проекте?
Я как понял. Program.cs здесь ничего не меняем из Вашего кода. А в simplex.cs меняем namespace Simplex на namespace имя проекта, правильно?
Правильно
Один фиг не получается )))
А если вот такая задача:
целевую функцию минимизировать:
801*x000 + 391*x001 + 705*x002 + 596*x010 + 472*x011 + 821*x012 + 490*x020 + 261*x021 + 710*x022 + 590*x100 + 322*x101 + 373*x102 + 496*x110 + 514*x111 + 600*x112 + 492*x120 + 405*x121 + 591*x122 + 632*x200 + 535*x201 + 533*x202 + 375*x210 + 564*x211 + 597*x212 + 288*x220 + 372*x221 + 505*x222
Ограничения
1*x000 + 1*x001 + 1*x002 + 1*x010 + 1*x011 + 1*x012 + 1*x020 + 1*x021 + 1*x022 = 1
1*x100 + 1*x101 + 1*x102 + 1*x110 + 1*x111 + 1*x112 + 1*x120 + 1*x121 + 1*x122 = 1
1*x200 + 1*x201 + 1*x202 + 1*x210 + 1*x211 + 1*x212 + 1*x220 + 1*x221 + 1*x222 = 1
1*x000 + 1*x001 + 1*x002 + 1*x100 + 1*x101 + 1*x102 + 1*x200 + 1*x201 + 1*x202 = 1
1*x010 + 1*x011 + 1*x012 + 1*x110 + 1*x111 + 1*x112 + 1*x210 + 1*x211 + 1*x212 = 1
1*x020 + 1*x021 + 1*x022 + 1*x120 + 1*x121 + 1*x122 + 1*x220 + 1*x221 + 1*x222 = 1
1*x000 + 1*x010 + 1*x020 + 1*x100 + 1*x110 + 1*x120 + 1*x200 + 1*x210 + 1*x220 = 1
1*x001 + 1*x011 + 1*x021 + 1*x101 + 1*x111 + 1*x121 + 1*x201 + 1*x211 + 1*x221 = 1
1*x002 + 1*x012 + 1*x022 + 1*x102 + 1*x112 + 1*x122 + 1*x202 + 1*x212 + 1*x222 = 1
x000 >= 0
x001 >= 0
x002 >= 0
x010 >= 0
x011 >= 0
x012 >= 0
x020 >= 0
x021 >= 0
x022 >= 0
x100 >= 0
x101 >= 0
x102 >= 0
x110 >= 0
x111 >= 0
x112 >= 0
x120 >= 0
x121 >= 0
x122 >= 0
x200 >= 0
x201 >= 0
x202 >= 0
x210 >= 0
x211 >= 0
x212 >= 0
x220 >= 0
x221 >= 0
x222 >= 0
Количество переменных и ограничений не влияет на алгоритм решения задачи. Так что можно попробовать решить ее с помощью программы.
А как построить матрицу с такой задачей? хотя бы напишите пожалуйста строку с целевой функцией и двумя различными ограничениями
Посмотрите выше мой ответ на комментарий Михаила (от 11.04.2017). И подобно его примеру можно построить матрицу.
Нужно учесть, что у вас задача минимизации, поэтому необходимо сделать min(f(x)) = max(-f(x)).
Поскольку в вашей задаче слишком много переменных, не будем писать здесь полную матрицу. Сокращенно примерно будет так:
1 1 1 …
1 1 1 …
…
0 801 391 …
Так и не смог понять, как нужно записать выражение вида =>. Можете привести пример?
Посмотрите мой комментарий от 20.12.2016 в 22:09. Там есть вся информация по данному вопросу.