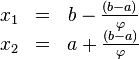В статье речь пойдет о методе золотого сечения и, соответственно, о нахождении с помощью этого метода экстремума функции на заданном отрезке. Для реализации алгоритма будет использован язык Java.
Метод золотого сечения — это итеративный метод поиска экстремумов (минимума или максимума) функции одной переменной на заданном отрезке [a; b]. Метод золотого сечения был продемонстрирован в 1953 году Джеком Кифером. В его основе лежит принцип деления отрезка в пропорции золотого сечения.
Теоретические сведения
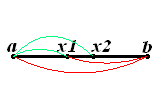
Пусть задана функция f(x) и отрезок [a; b], на котором требуется найти экстремум. Рассматриваемый отрезок делится в оба направления точками x1 и x2 в отношении золотого сечения. То есть:
φ — это пропорция золотого сечения.
Следовательно координаты x1 и x2 находятся по формулам:
Таким образом точки x1 и x2 делят отрезки [a; x2] и [x1; b] соответственно в пропорции золотого сечения. Это свойство далее будет использоваться для построения итеративного процесса вычисления экстремума функции.
Описание алгоритма
- Задаются начальные параметры: границы отрезка [a; b] и точность вычислений ε.
- Рассчитываются координаты точек деления:
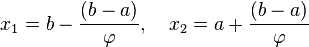. Затем вычисляется значение функции f(x) в этих точках: 
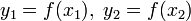. ЕСЛИ 
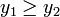(случай поиска минимума функции. Для поиска точки максимума изменить неравенство на 
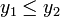), ТО 
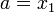. ИНАЧЕ 
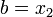. - ЕСЛИ требуемая точность достигнута:
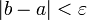, ТО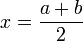 
и конец алгоритма. ИНАЧЕ возврат к шагу 2.
Реализация алгоритма
Напишем программу, реализующую приведенный выше алгоритм метода золотого сечения. Также приведем пример поиска экстремума для конкретной функции. Разработку будем вести на языке программирования JAVA.
Класс GoldenSection, позволяющий выполнить поиск экстремума функции на отрезке [a; b] с точностью ε, содержит (по порядку): определение константы пропорции золотого сечения φ, метод, вычисляющий значение целевой функции f(x), метод, выполняющий поиск минимума функции и метод, выполняющий поиск максимума функции.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
class GoldenSection{ final double PHI = (1 + Math.sqrt(5)) / 2; double f(double x){ return Math.pow(x + 1, 3) + 5 * Math.pow(x, 2); } double findMin(double a, double b, double e){ double x1, x2; while (true){ x1 = b - (b - a) / PHI; x2 = a + (b - a) / PHI; if (f(x1) >= f(x2)) a = x1; else b = x2; if (Math.abs(b - a) < e) break; } return (a + b) / 2; } double findMax(double a, double b, double e){ double x1, x2; while (true){ x1 = b - (b - a) / PHI; x2 = a + (b - a) / PHI; if (f(x1) <= f(x2)) a = x1; else b = x2; if (Math.abs(b - a) < e) break; } return (a + b) / 2; } } |
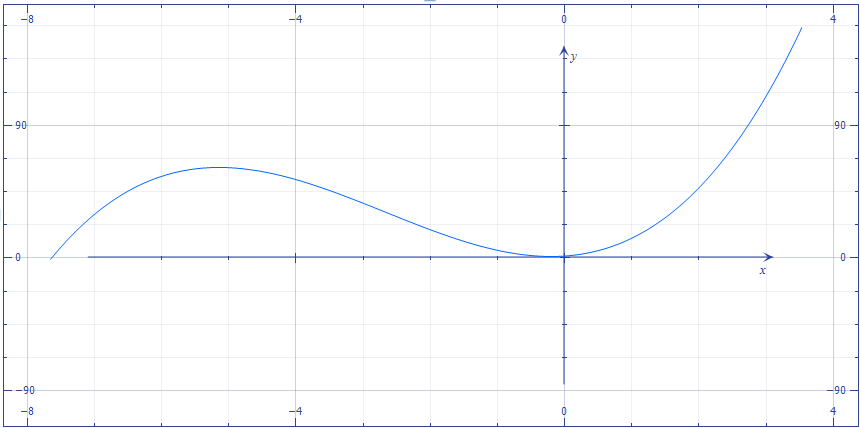
Пример. Выполним поиск минимума и максимума функции 
на отрезках [-2; 2] и [-8; 0] соответственно. Вычисления будем производить с точностью ε = 0.001.
График функции f(x):
|
1 2 3 4 5 6 7 8 9 |
public class GoldenSectionMethod { public static void main(String[] args) { GoldenSection GS = new GoldenSection(); System.out.println(GS.findMin(-2, 2, 0.001)); System.out.println(GS.findMax(-8, 0, 0.001)); } } |
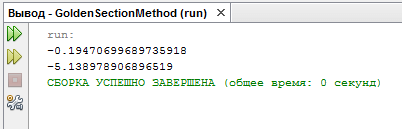
Результат работы программы:
Для того чтобы скачать исходник программы, написанной в NetBeans, нажмите на кнопку:
Скачать исходник
Поделиться в соц. сетях: