В статье покажем, как найти точку пересечения отрезков. Это совсем не тривиальная задача, хотя на первый взгляд она кажется именно такой. Поиск пересечения двух отрезков имеет множество полезных приложений. Например, с помощью него можно определить пересекаются ли фигуры на плоскости или нет.
Начальные условия
На протяжении всей статьи мы будем писать метод, который ищет пересечение двух отрезков на плоскости и даёт ответ: пересекаются они или нет.
Входными параметрами метода являются 4 точки — точки начала и конца двух отрезков.
Точка — это экземпляр класса Point. Она имеет два параметра: значение абсциссы (x) и значение ординаты (y). Класс Point:
|
1 2 3 4 5 6 7 8 9 10 |
public class Point { double x, y; public Point (double newX, double newY) { x = newX; y = newY; } } |
Поиск пересечения двух отрезков
Метод, который будет искать пересечение двух отрезков, назовём: checkIntersectionOfTwoLineSegments. Он возвращает true, если отрезки пересекаются и false в противном случае.
|
1 2 |
private boolean checkIntersectionOfTwoLineSegments(Point p1, Point p2, Point p3, Point p4) { |
Его аргументы — это четыре точки. p1 и p2 — начало и конец первого отрезка, а p3 и p4 — соответственно начало и конец второго отрезка.
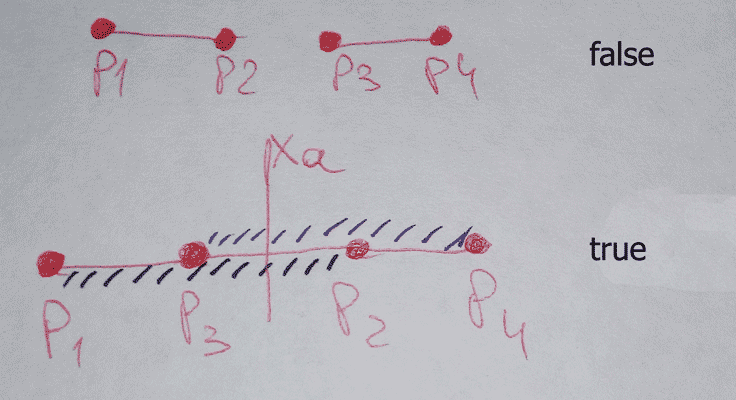
Мы подразумеваем, что начальная точка находится левее конечной относительно оси абсцисс (оси X). Также возможен вариант, когда точки имеют одинаковую абсциссу, то есть отрезок является вертикальным.
В общем случае должно выполняться условие: p1.x <= p2.x и p3.x <= p4.x.
Но если вдруг программист задал точки отрезка не по порядку, мы расставим их, как следует:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
if (p2.x < p1.x) { Point tmp = p1; p1 = p2; p2 = tmp; } if (p4.x < p3.x) { Point tmp = p3; p3 = p4; p4 = tmp; } |
После того, как точки отрезков расставлены по порядку, мы можем сразу проверить наличие потенциального интервала, на котором отрезки могут пересекаться.
Если конец первого отрезка находится левее начала правого отрезка (по оси X), то отрезки точно не имеют точки пересечения.
|
1 2 3 |
if (p2.x < p3.x) { return false; } |
Потенциальный интервал пересечения имеется. Идём далее.
Оба отрезка вертикальные (частный случай)
Мы отдельно от общего решения будем рассматривать вертикальные отрезки, поскольку тангенс 90 градусов не определён, и, тем самым, мы в общем решении избежим деления на ноль.
Сначала обсудим такой частный случай, когда оба отрезка являются вертикальными.
Отрезок вертикальный, тогда и только тогда, когда абсциссы его обеих точек равны.
В случае проверки условия вертикальности обоих отрезков, выражение (p1.x — p2.x == 0) && (p3.x — p4.x == 0) должно быть истинным.
Два отрезка будут иметь точку пересечения в том случае, когда их абсцисса одинакова (для этого достаточно условия p1.x == p3.x) и они имеют общую часть по оси ординат (общий Y); в противном случае делаем вывод, что они не пересекаются.
Составить условие для проверки существования общего Y мысленно довольно сложно. Поэтому мы поступим проще: составим условие для проверки того, что отрезки не имеют общего Y и возьмём от него отрицание.
Напишем код на Java для всего вышесказанного:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
//если оба отрезка вертикальные if((p1.x - p2.x == 0) && (p3.x - p4.x == 0)) { //если они лежат на одном X if(p1.x == p3.x) { //проверим пересекаются ли они, т.е. есть ли у них общий Y //для этого возьмём отрицание от случая, когда они НЕ пересекаются if (!((Math.max(p1.y, p2.y) < Math.min(p3.y, p4.y)) || (Math.min(p1.y, p2.y) > Math.max(p3.y, p4.y)))) { return true; } } return false; } |
Решаем систему уравнений и находим точку пересечения отрезков
Каждый отрезок — это часть прямой. Уравнение прямой в общем случае имеет всем нам знакомый вид:
A * x + b = y (1)
Для случая с двумя прямыми получаем систему уравнений (2):
A1 * x + b1 = y
A2 * x + b2 = y
Решив её, мы получим координаты точки (x, y) пересечения двух прямых. Но у нас нет значений параметров A1, A2, b1 и b2. Найдём их.
Параметр A — это тангенс угла между прямой и осью X. Вычислим его по определению: тангенс — это отношение противолежащего катета к прилежащему.
A1 = (p1.y — p2.y) / (p1.x — p2.x) (3)
A2 = (p3.y — p4.y) / (p3.x — p4.x) (4)
Параметр b найдём для каждой прямой, выразив его из уравнений (2):
b1 = p1.y — A1 * p1.x = p2.y — A1 * p2.x (5)
b2 = p3.y — A2 * p3.x = p4.y — A2 * p4.x (6)
Теперь, зная все параметры, решим систему уравнений (2). Найдём абсциссу точки пересечения прямых (обозначим её Xa):
Xa = (b2 — b1) / (A1 — A2) (7)
Как практически в любом решении и, к сожалению, здесь тоже есть частные случаи, о которых следует поговорить отдельно.
При нахождении параметров A1 и A2 (уравнения 3, 4) может возникнуть исключительная ситуация деления на ноль. Такое возможно, когда один из отрезков вертикальный.
Один из отрезков вертикальный (частный случай)
Сначала рассмотрим ситуацию, когда первый отрезок вертикальный.
Предположим, что x вертикального отрезка является абсциссой точки пересечения отрезков: Xa = p1.x. Параметры A2 и b2 найдём, как это было описано выше. Также вычислим ординату предполагаемой точки пересечения (используя формулу 1):
Ya = A2 * Xa + b2
Найденная точка (Xa, Ya) будет являться точкой пересечения двух отрезков только в том случае, если p3.x <= Xa <= p4.x и Ya входит в интервал вертикального отрезка по Y. В противном случае — отрезки не пересекаются.
Оформим всё вышесказанное в этом подпункте в виде кода:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
//если первый отрезок вертикальный if (p1.x - p2.x == 0) { //найдём Xa, Ya - точки пересечения двух прямых double Xa = p1.x; double A2 = (p3.y - p4.y) / (p3.x - p4.x); double b2 = p3.y - A2 * p3.x; double Ya = A2 * Xa + b2; if (p3.x <= Xa && p4.x >= Xa && Math.min(p1.y, p2.y) <= Ya && Math.max(p1.y, p2.y) >= Ya) { return true; } return false; } |
Когда второй отрезок является вертикальным — это тоже частный случай, который должен быть рассмотрен. Аналогично:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
//если второй отрезок вертикальный if (p3.x - p4.x == 0) { //найдём Xa, Ya - точки пересечения двух прямых double Xa = p3.x; double A1 = (p1.y - p2.y) / (p1.x - p2.x); double b1 = p1.y - A1 * p1.x; double Ya = A1 * Xa + b1; if (p1.x <= Xa && p2.x >= Xa && Math.min(p3.y, p4.y) <= Ya && Math.max(p3.y, p4.y) >= Ya) { return true; } return false; } |
Оба отрезка невертикальные (общий случай)
Сначала найдём параметры A1, A2, b1 и b2 по формулам 3, 4, 5, 6.
Затем проверим равенство A1 == A2. Если оно верно, то значит отрезки параллельны, а следовательно не пересекаются — возвращаем false. Кроме того, данная проверка позволяет избежать деления на ноль при нахождении Xa в выражении 7.
Далее вычисляем Xa (по формуле 7).
После необходимо проверить входит ли Xa в пересечение проекций обоих отрезков на ось X. Входит — возвращаем true, не входит — false.
Код на Java:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
//оба отрезка невертикальные double A1 = (p1.y - p2.y) / (p1.x - p2.x); double A2 = (p3.y - p4.y) / (p3.x - p4.x); double b1 = p1.y - A1 * p1.x; double b2 = p3.y - A2 * p3.x; if (A1 == A2) { return false; //отрезки параллельны } //Xa - абсцисса точки пересечения двух прямых double Xa = (b2 - b1) / (A1 - A2); if ((Xa < Math.max(p1.x, p3.x)) || (Xa > Math.min( p2.x, p4.x))) { return false; //точка Xa находится вне пересечения проекций отрезков на ось X } else { return true; } |
Написание метода для нахождения точки пересечения двух отрезков завершено.
|
1 |
} |
Скачать его полностью в текстовом файле:
Скачать код метода
Приложения
Написанный в статье метод можно использовать для определения пересечения плоских фигур. Фигуры должны состоять из замкнутой ломаной линии, то есть состоять из отрезков. Это могут быть треугольники, прямоугольники, либо другие произвольные фигуры.
Чтобы определить пересечение двух фигур, нужно проверить пересечение каждой стороны одной фигуры с каждой стороной другой фигуры. Если хотя бы одна сторона с чем-то пересекается — значит и фигуры пересекаются.
Например, если нужно определить пересекаются ли прямоугольники, то необходимо будет выполнить 16 проверок.
Спасибо за прочтение статьи!
Поделиться в соц. сетях:
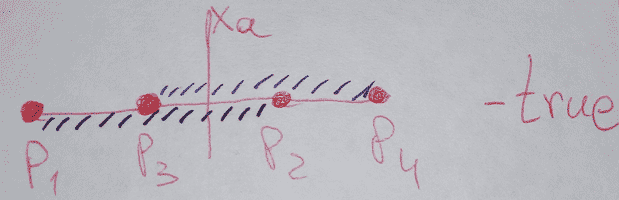
Спасибо огромное, наконец-то я нашел код который реально работает и в любой ситуации