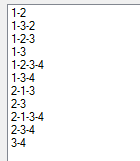В этой статье речь пойдет об алгоритме поиска всех элементарных цепей в неориентированном графе. Будет приведено описание алгоритма и его реализация на языке программирования C#.
Цепью в графе называется последовательность ребер 
, когда каждое предыдущее ребро 
соприкасается одним из своих концов со следующим ребром 
. Цепь обозначается последовательностью вершин, которые она содержит (2-5-3-6).
Цепь называется элементарной, если все вершины, входящие в нее, различны.
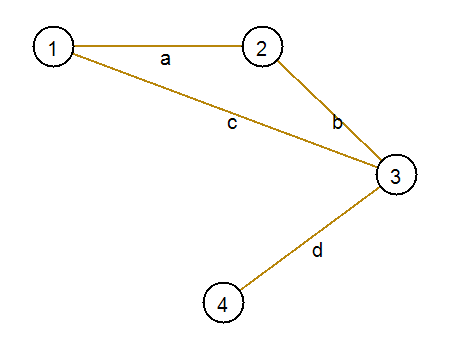
Приведем пример. Пусть дан граф, как на рисунке ниже:
Все элементарные цепи в нем: 1-2, 1-3-2, 1-2-3, 1-3, 1-2-3-4, 1-3-4, 2-1-3, 2-3, 2-1-3-4, 2-3-4, 3-4.
Пусть граф задан, как G = (V, E), где V — множество вершин графа, а E — множество его ребер. Вершины и ребра можно представить объектами следующих классов:
|
1 2 3 4 5 6 7 8 9 10 11 |
//вершина class Vertex { public int x, y; public Vertex(int x, int y) { this.x = x; this.y = y; } } |
, где x, y — координаты вершины на плоскости.
|
1 2 3 4 5 6 7 8 9 10 11 |
//ребро class Edge { public int v1, v2; public Edge(int v1, int v2) { this.v1 = v1; this.v2 = v2; } } |
, где v1, v2 — номера вершин, которые соединяет ребро.
Множество вершин и ребер можно хранить в виде списков:
|
1 2 |
List<Vertex> V; List<Edge> E; |
Для поиска всех элементарных цепей модифицируем рекурсивный алгоритм «поиск в глубину» (DFS) — это один из алгоритмов обхода графа. Подробнее про него можно почитать здесь.
Модифицируем алгоритм DFS в DFSchain.
|
1 |
DFSchain(int u, int endV, List<Edge> E, int[] color, string s) |
, где u — номер начальной вершины цепи, endV — номер конечной вершины цепи, Е — список ребер, color[] — массив, в котором хранятся цвета вершин, s — строка, в которую записывается последовательность вершин искомой цепи.
Хранить результаты поиска будем в списке строк:
|
1 |
List<string> chains; |
Приведем описание DFSchain. В начальный момент времени все вершины графа окрашены в белый цвет. Требуется выполнить следующее:
Перебираем все пары вершин, возможно, они являются началом и концом цепи. На каждой итерации перекрашиваем все вершины в белый цвет (обозначим его 1, а черный цвет будем обозначать 2). Вызываем процедуру DFSchain(…).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
private void chainsSearch() { int[] color = new int[V.Count]; for (int i = 0; i < V.Count - 1; i++) for (int j = i + 1; j < V.Count; j++) { for (int k = 0; k < V.Count; k++) color[k] = 1; DFSchain(i, j, E, color, (i + 1).ToString()); //поскольку в C# нумерация элементов начинается с нуля, то //для удобочитаемости результатов в строку передаем i + 1 } } |
Процедура DFSchain(int u, int endV, List<Edge> E, int[] color, string s).
- Если номер вершины u не равен endV, значит мы не достигли конца цепи, поэтому перекрашиваем вершину u в черный цвет. Иначе — конец цепи достигнут: добавляем цепь s в список и выполняем возврат из функции.
- Для всякой вершины w, смежной с вершиной u и окрашенной в белый цвет, рекурсивно выполняем процедуру DFSchain(w, endV, E, color, s + «-» + (w + 1).ToString()). Возвращаем вершине w белый цвет (возможно через нее проходят другие цепи, поэтому не будем исключать ее из рассмотрения).
Приведем реализацию процедуры DFSchain на языке C#:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
private void DFSchain(int u, int endV, List<Edge> E, int[] color, string s) { //вершину не следует перекрашивать, если u == endV (возможно в endV есть несколько путей) if (u != endV) color[u] = 2; else { chains.Add(s); return; } for (int w = 0; w < E.Count; w++) { if (color[E[w].v2] == 1 && E[w].v1 == u) { DFSchain(E[w].v2, endV, E, color, s + "-" + (E[w].v2 + 1).ToString()); color[E[w].v2] = 1; } else if (color[E[w].v1] == 1 && E[w].v2 == u) { DFSchain(E[w].v1, endV, E, color, s + "-" + (E[w].v1 + 1).ToString()); color[E[w].v1] = 1; } } } |
Результатом выполнения этой процедуры поиска для графа, рассмотренного выше, будет такая последовательность цепей:
Поделиться в соц. сетях: