Программирование на C, C# и Java

В этой статье рассмотрим одну из важнейших задач структурного анализа — топологическую декомпозицию структуры системы, то есть выделение в ней сильно связных подграфов (подсистем). Будет описан алгоритм и приведена его реализация на языке программирования C#.

Теоретические сведения

Введем некоторые определения. Множество вершин графа G(V, E), достижимых из вершины i, называется достижимым множеством R(i) и определяется следующим образом:

где G(i) — множество правых инциденций вершины i, т. е. множество вершин, достижимых из вершины i с использованием путей длиной, равной единице; G(P)(i) — множество вершин, достижимых из вершины i с использованием путей длиной p. При этом предполагается, что сама вершина i достижима с использованием пути длиной, равной нулю, и включена во множество R(i).

Контрдостижимым множеством Q(i) графа G(V, E) называется множество таких вершин, когда из любой вершины этого множества можно достигнуть вершины i. Оно определяется следующим образом:

где G(-1)(i) — множество левых инциденций вершины i, т. е. множество вершин, из которых можно достичь i-ую вершину, при этом длина пути равна 1 и т. д.

Пересечение множеств R(i) ∩ Q(j) — это множество таких вершин, каждая из которых принадлежит по крайней мере одному пути, идущему от i-ой вершины к j-ой. Эти вершины называются существенными или неотъемлемыми, относительно двух концевых вершин i и j.

Множество R(i) ∩ Q(i) — однозначно определяет сильно связный подграф графа G(V, E), содержащий вершину i, т.к. все вершины этого множества достижимы из i-ой вершины и из каждой вершины достижима вершина i, то есть они взаимно достижимы.

Описание алгоритма

1. Выбираем вершину с наименьшим номером i.
2. Определяем для нее достижимое множество вершин R(i).
3. Определяем для нее контрдостижимое множество вершин Q(i).
4. Выделяем в системе сильно связный подграф, включающий множество вершин V = R(i) ∩ Q(i).
5. Удаляем все вершины V из первоначального графа.
6. ЕСЛИ начальный граф не пуст, ТО переходим к шагу 1. ИНАЧЕ конец.

Пример использования алгоритма

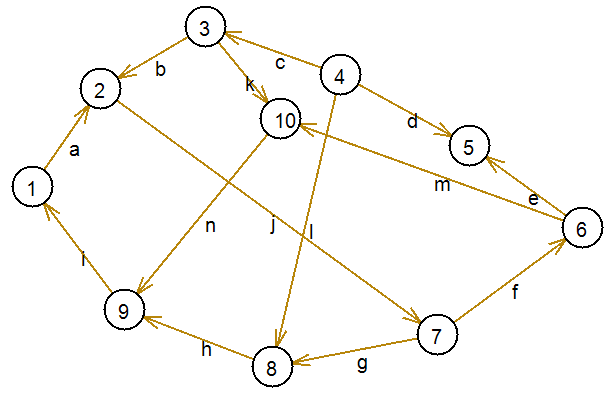
Пусть имеется такой граф:

1. Определяем достижимое множество для вершины 1: R(1) = (1, 2, 5, 7, 6, 8, 9, 10).
2. Определяем контрдостижимое множество для вершины 1: Q(1) = (1, 9, 8, 10, 3, 6, 4, 7, 2).
3. Находим пересечение этих множеств, которое и определяет сильно связный подграф (подсистему), включающий вершину 1: V1 = R(1) ∩ Q(1) => G1(V1, E1) = (1, 2, 6, 7, 8, 9, 10).
4. Удаляем все вершины V1 из первоначального графа.
5. Поступаем аналогично с остальными вершинами:

V2 = R(3) ∩ Q(3) => G2(V2, E2) = (3),

V3 = R(4) ∩ Q(4) => G3(V3, E3) = (4),

V4 = R(5) ∩ Q(5) => G4(V4, E4) = (5).

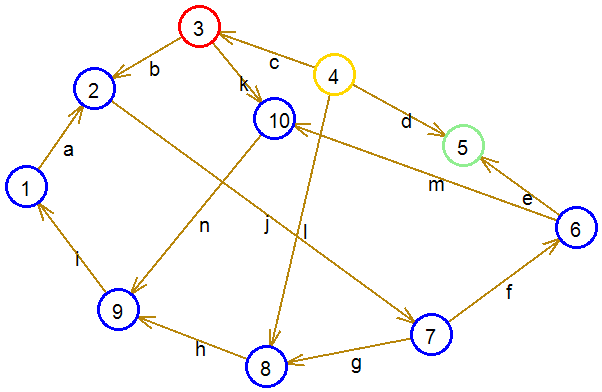
В результате декомпозиции получили 4 связных подграфа (подсистемы): G1 (1, 2, 6, 7, 8, 9, 10), G2 (3), G3 (4), G4 (5).

Реализация алгоритма

Рассмотрим реализацию алгоритма топологической декомпозиции на языке программирования C#.

Пусть дуга графа представлено экземпляром класса Edge:

, где v1 – номер вершины, из которой дуга исходит, а v2 — номер вершины, в которую данная дуга заходит.

Подграф представим в виде экземпляра класса Subgraph:

, где List<int> V — список номеров вершин, входящих в подграф.

Все множества дуг и подграфов будем хранить в виде списков:

Приведем реализацию метода topologicalDecomposition(…), выполняющего топологическую декомпозицию структуры.

Аргументы метода topologicalDecomposition: countV — количество вершин в графе, E — список дуг в графе, Sub — список подграфов.

Для обхода графа и поиска множеств R и Q используется рекурсивный алгоритм «Поиск в глубину» (Depth-first search). Опишем принцип его работы:

Пусть дан граф G = (V, E), где V — множество вершин графа, E — множество его ребер. Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним следующие действия:

1. Переберем все вершины v ∈ V. ЕСЛИ вершина белая, выполним для нее DFS(v).

Процедура DFS (параметр — вершина u ∈ V)

1. Перекрашиваем вершину u в черный цвет.
2. Для всякой вершины w, смежной с вершиной u и окрашенной в белый цвет, рекурсивно выполняем процедуру DFS(w).

Вот реализация метода DFS для нашей задачи (белый цвет — это 1, черный — 2):

Аргументы метода DFS: u — номер начальной вершины, endV — номер конечной вершины, E — список дуг графа, color — цвета вершин. Если вершина endV достижима из вершины u, то метод вернет значение true, иначе false.

Скачать листинги из статьи