Существует замечательный универсальный алгоритм балансировки АВЛ-дерева (AVL), который охватывает сразу все возможные случаи нарушения сбалансированности дерева. Данный алгоритм называется трехузловая реструктуризация (англ. Trinode Restructuring) и в российской литературе почему-то практически не встречается.
Что такое АВЛ-дерево
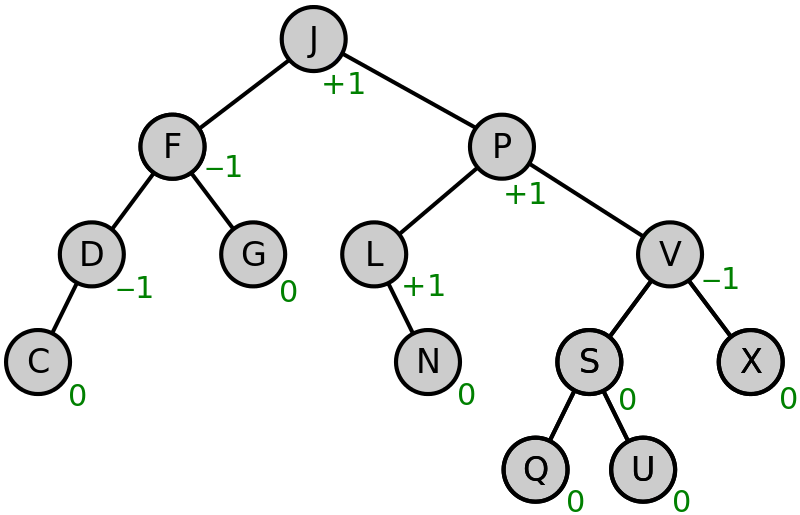
АВЛ-дерево — это сбалансированное двоичное дерева поиска. Сбалансированность выражается в том, что высота левого и правого поддеревьев каждой вершины отличается не более чем на единицу.
Каждая вершина AVL-дерева характеризуется показателем под названием balance factor (разница между высотой правого и левого поддерева). У узлов сбалансированного дерева он равен -1, 0 или 1.
Если при добавлении новой вершины или удалении существующей balance factor становится равным -2 или 2, то требуется балансировка дерева.
Алгоритм балансировки АВЛ-дерева
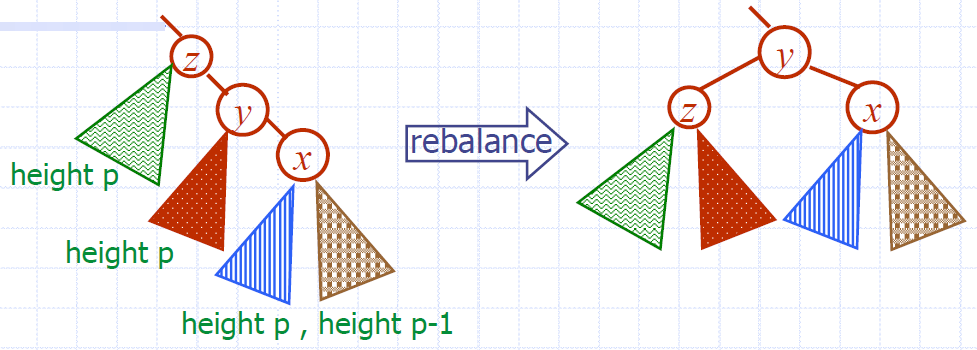
Всего существует четыре варианта разбалансировки AVL-дерева. Вариант 1:
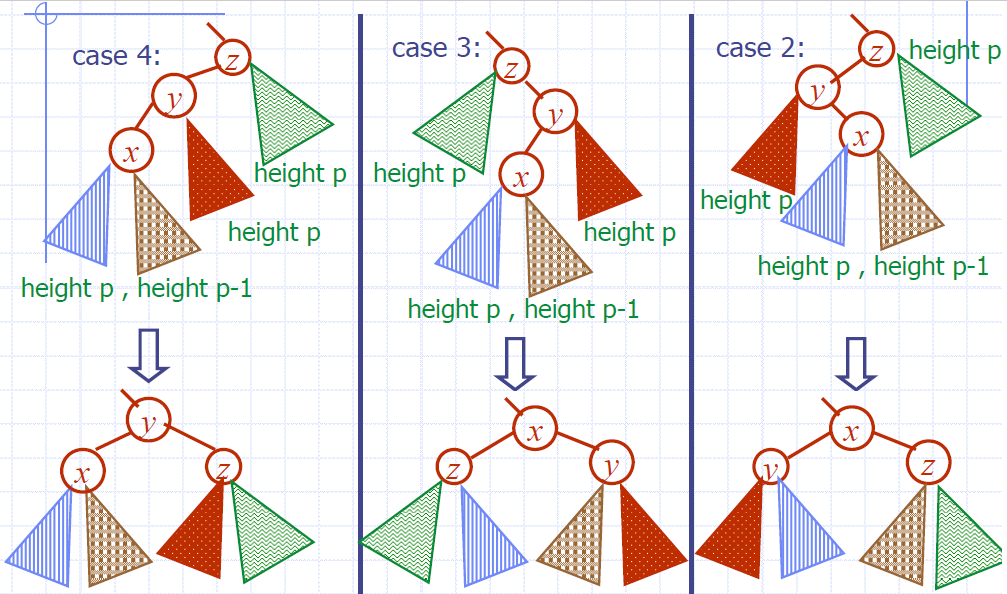
Варианты 2, 3 и 4:
Во всех четырех вариантах используется один и тот же алгоритм балансировки АВЛ-дерева, под названием трехузловая реструктуризация (англ. Trinode Restructuring).
Для узлов x, y, z:
- Выбираем из трех вершин ту, которая имеет медианное значение ключа. Данная вершина будет новым узлом-родителем.
- Узел с наименьшим значением ключа будет его левым потомком.
- Узел с наибольшим значением ключа будет его правым потомком.
- Прежних потомков нового узла-родителя нужно разместить так:
Левое поддерево (если оно было и не равно связи с новыми потомками) становится правым поддеревом нового левого узла.
Правое поддерево (если оно было и не равно связи с новыми потомками) становится левым поддеревом нового правого узла.
Процедура балансировки начинается из глубины дерева и продолжается до тех пор, пока все AVL-дерево не станет сбалансированным.
Поделиться в соц. сетях: