Метод хорд используется для численного нахождения приближенного значения корня нелинейного уравнения. В данной статье будет показан алгоритм метода, а также будет приведена его программная реализация на языках: Си, C# и Java.
Метод хорд (то же, что метод секущих) — итерационный метод решения нелинейного уравнения.
Нелинейное уравнение — это уравнение в котором есть хотя бы один член, включающий неизвестное, НЕ в первой степени. Обозначается, как: f(x) = 0.
Метод хорд. Алгоритм
Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной.
Итерационная формула для вычислений методом хорд следующая:
Вычисления продолжаются до тех пор, пока не станет истинным выражение:
|x(k+1) — xk| ≤ ε
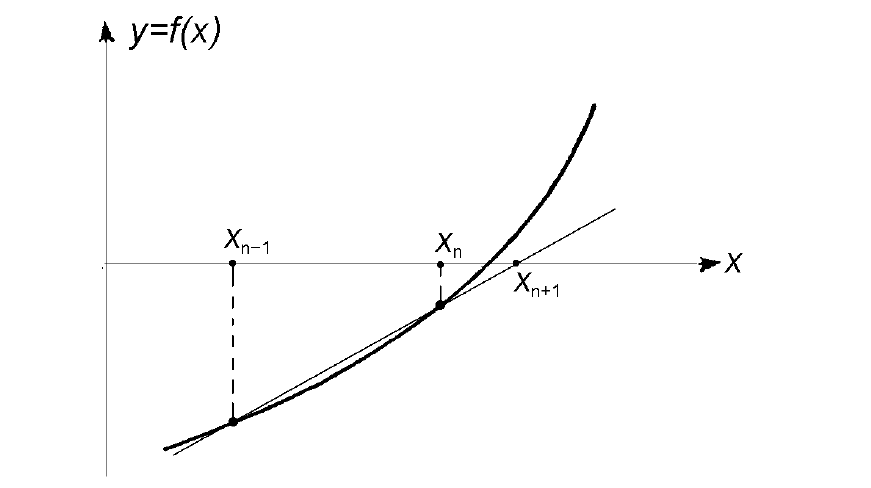
Геометрическая модель одного шага итераций метода хорд представлена на рисунке:
Метод хорд, в отличие от метода Ньютона, имеет плюс в том, что для расчета не требуется вычисление производных. Но при этом метод хорд медленнее, его сходимость равна золотому сечению:
Метод хорд. Программная реализация
Ниже мы приводим реализацию алгоритма метода хорд на языках программирования Си, C# и Java. Кроме того, исходники программ доступны для скачивания.
В качестве примера ищется корень уравнения x3 — 18x — 83 = 0 в области x0 = 2, x1 = 10, с погрешностью e = 0.001. (Корень равен: 5.7051).
x_prev — это xk-1, x_curr — это xk, x_next — это xk+1.
Блок-схема алгоритма метода хорд:
Язык Си
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
#include <stdio.h> #include <math.h> #include <conio.h> double method_chord(double x_prev, double x_curr, double e); double f(double x); int main() { double x0 = 2; double x1 = 10; double e = 0.001; double x = method_chord(x0, x1, e); printf("%f", x); _getch(); return 0; } double method_chord(double x_prev, double x_curr, double e) { double x_next = 0; double tmp; do { tmp = x_next; x_next = x_curr - f(x_curr) * (x_prev - x_curr) / (f(x_prev) - f(x_curr)); x_prev = x_curr; x_curr = tmp; } while (abs(x_next - x_curr) > e); return x_next; } double f(double x) { return pow(x, 3) - 18 * x - 83; } |
Язык C#
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace metodHord { class Program { static void Main(string[] args) { double x0 = 2; double x1 = 10; double e = 0.001; double x = method_chord(x0, x1, e); Console.WriteLine(x); Console.ReadLine(); } public static double method_chord(double x_prev, double x_curr, double e) { double x_next = 0; double tmp; do { tmp = x_next; x_next = x_curr - f(x_curr) * (x_prev - x_curr) / (f(x_prev) - f(x_curr)); x_prev = x_curr; x_curr = tmp; } while (Math.Abs(x_next - x_curr) > e); return x_next; } public static double f(double x) { return Math.Pow(x, 3) - 18 * x - 83; } } } |
Язык Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
package metodhord; public class MetodHord { public static void main(String[] args) { double x0 = 2; double x1 = 10; double e = 0.001; double x = method_chord(x0, x1, e); System.out.println(x); } public static double method_chord (double x_prev, double x_curr, double e) { double x_next = 0; double tmp; do{ tmp = x_next; x_next = x_curr - f(x_curr) * (x_prev - x_curr) / (f(x_prev) - f(x_curr)); x_prev = x_curr; x_curr = tmp; } while (Math.abs(x_next - x_curr) > e); return x_next; } public static double f (double x){ return Math.pow(x, 3) - 18 * x - 83; } } |
Поделиться в соц. сетях:
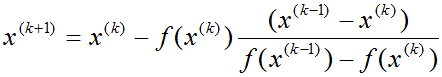

В варианте для языка С допущена ошибка:
Необходимо в цикле while использовать не abs(), a fabs() ибо код работает некорректно при слишком высоких требованиях точности.