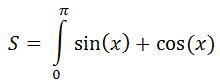В этой статье мы рассмотрим вычисление интеграла на языке Си. Будет приведён теоретический материал и его реализация в виде программы.
Для того, чтобы найти значение интеграла, нам понадобится формула парабол (Симпсона) — это один из самых точных численных методов для нахождения определенного интеграла. Вот эта формула:
где h = (b-a)/2n, 2n — количество отрезков (четное число), на которое мы делим интервал интегрирования (чем больше, тем точнее вычисления).
В скобках формулы вычисления интеграла мы видим, как сгруппированы значения функции: первое и последнее просто суммируются, значения с нечетными индексами умножаются на 4, а с четными на 2.
Напишем программу, которая вычисляет такой определенный интеграл:
Подключим необходимые библиотеки и определим константу N — число отрезков (четное), на которое мы будет делить отрезок интегрирования [a, b]:
|
1 2 3 4 5 |
#include <stdio.h> #include <math.h> #include <conio.h> #define N 10000 |
Нам понадобится функция F(double x), вычисляющая значение sin(x) + cos(x), она будет возвращать значение типа double — вещественный тип повышенной точности:
|
1 2 3 4 5 6 |
double F (double x) { double f; f = sin(x) + cos(x); return f; } |
Переходим к функции main(). Определим необходимые переменные, константу Пи и вычислим значение h:
|
1 2 3 4 5 6 |
double S = 0, x, a, b, h; const double Pi = 3.14159; a = 0; b = Pi; //отрезок [a, b] разобьем на N частей h = (b - a)/N; |
Вычисляем значение x1 и в цикле начинаем вычислять часть формулы .. + 4(…) + 2(…):
|
1 2 3 4 5 6 7 8 9 10 |
x = a + h; while (x < b) { S = S + 4*F(x); x = x + h; //проверяем не вышло ли значение x за пределы полуинтервала [a, b) if (x >= b) break; S = S + 2*F(x); x = x + h; } |
Добавляем к S первое и последнее значение функции S + f(a) + f(b) и умножаем результат на (h/3). Выводим результат в консоль:
|
1 2 3 4 |
S = (h/3)*(S + F(a) + F(b)); printf ("%f", S); _getch (); return 0; |
В итоге получается такая программа (исходник, как обычно, можно скачать внизу страницы):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
#include <stdio.h> #include <math.h> #include <conio.h> #define N 10000 double F (double x) { double f; f = sin(x) + cos(x); return f; } int main () { double S = 0, x, a, b, h; const double Pi = 3.14159; a = 0; b = Pi; //отрезок [a, b] разобьем на N частей h = (b - a)/N; x = a + h; while (x < b) { S = S + 4*F(x); x = x + h; //проверяем не вышло ли значение x за пределы полуинтервала [a, b) if (x >= b) break; S = S + 2*F(x); x = x + h; } S = (h/3)*(S + F(a) + F(b)); printf ("%f", S); _getch (); return 0; } |
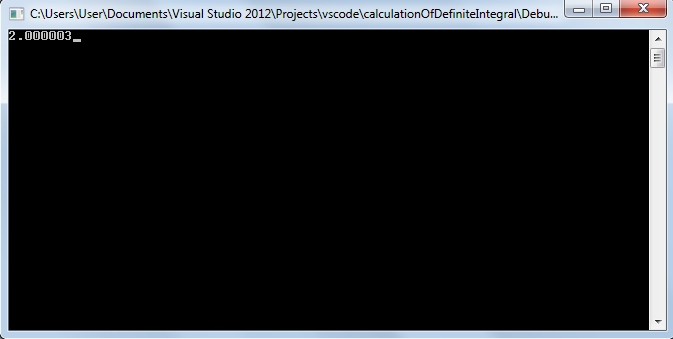
Демонстрация работы программы:
Значение интеграла равно двум!
Скачать исходникПоделиться в соц. сетях: