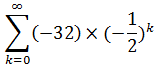В этом уроке мы расскажем как вычислить сумму бесконечного сходящегося ряда (последовательности) с определенной точностью. Будет рассмотрена соответствующая программа, написанная на языке программирования Си. В конце статьи можно скачать исходник этой программы для Visual Studio.
Сходящийся ряд — это числовая последовательность элементов множества X, имеющая предел в этом множестве.
Рассмотрим задачу вычисления суммы сходящегося ряда с определенной точностью на примере. Пусть дан ряд:
Вычисление суммы ряда с определенной точностью ε означает, что сумма ряда вычисляется до тех пор, пока модуль разности между текущим и предыдущим членом последовательности больше ε. В виде формулы это утверждение можно записать так: |an — an-1| > ε, то есть пока это выражение истинно, вычисления продолжаются.
Сначала напишем на языке Си функцию, которая будет вычислять и возвращать значение k-го члена ряда по переданному в нее значению k.
|
1 2 3 4 5 6 7 |
double f(int k) { double res; res = -32.0; res *= (double)powf(-0.5, k); return res; } |
res — это переменная вещественного типа повышенной точности double, в которую будет записан результат вычисления k-го члена ряда. Это же значение и будет возвращаться функцией.
Выражение res *= (double)powf(-0.5, k); эквивалентно выражению res = res * (double)powf(-0.5, k);
Оператор powf — это оператор возведения числа в степень. В нашем случае он вычисляет: -0.5k.
Функцию f можно записать короче:
|
1 2 3 4 |
double f(int k) { return -32.0 * powf(-0.5, k); } |
Теперь перейдем к функции main. Для начала считаем с консоли число e — это и будет заданная точность вычислений ε.
|
1 2 3 |
float e; printf("e = "); scanf_s("%f", &e); |
Объявим переменные, в которых будут хранится: значение предыдущего, значение текущего члена ряда, сумма ряда и номер текущего члена ряда (число k) соответственно.
|
1 2 3 |
double previous, current; double sum = 0; int k = 0; |
Отдельно вычислим первый член ряда (потом он станет «предыдущим»), чтобы затем перейти к вычислениям в цикле.
|
1 2 3 |
current = f(k); sum += current; k++; |
Запись выражения sum += current; эквивалентна записи: sum = sum + current;
Теперь перейдем к вычислениям в цикле. Условием выхода из цикла будет ложность выражения: |an — an-1| > ε.
|
1 2 3 4 5 6 7 |
do { previous = current; current = f(k); sum += current; k++; } while (abs(current - previous) > e); |
Сумма посчитана. Осталось вывести результат вычислений в консоль.
|
1 |
printf("sum = %f\n", sum); |
В итоге код программы с необходимыми подключенными библиотеками будет выглядеть следующим образом:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
#include <stdio.h> #include <math.h> #include <conio.h> double f(int k) { double res; res = -32.0; res *= (double)powf(-0.5, k); return res; } int main() { float e; printf("e = "); scanf_s("%f", &e); double previous, current; double sum = 0; int k = 0; current = f(k); sum += current; k++; do { previous = current; current = f(k); sum += current; k++; } while (abs(current - previous) > e); printf("sum = %f\n", sum); _getch(); return 0; } |
Оператор _getch(); в строке 34 нужен для того, чтобы консоль не закрывалась сразу по завершении исполнения программы.
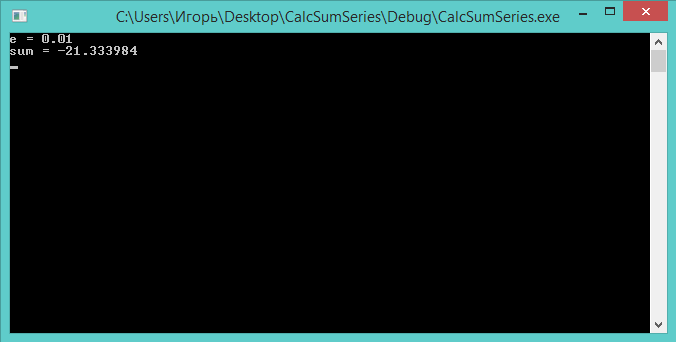
Демонстрация работы программы для нашего ряда представлена на скриншоте ниже. Точность вычислений составляет: ε = 0.01.
Скачать исходник
Поделиться в соц. сетях: