Представляем вашему вниманию программу для построения графов, написанную на языке C#. Внизу страницы вы можете скачать исходник этой программы, а в этой статье будут описаны функции программы и основные приемы, использовавшиеся при их кодировании.
Структура пользовательского интерфейса
Рисунок 1. Пользовательский интерфейс программы
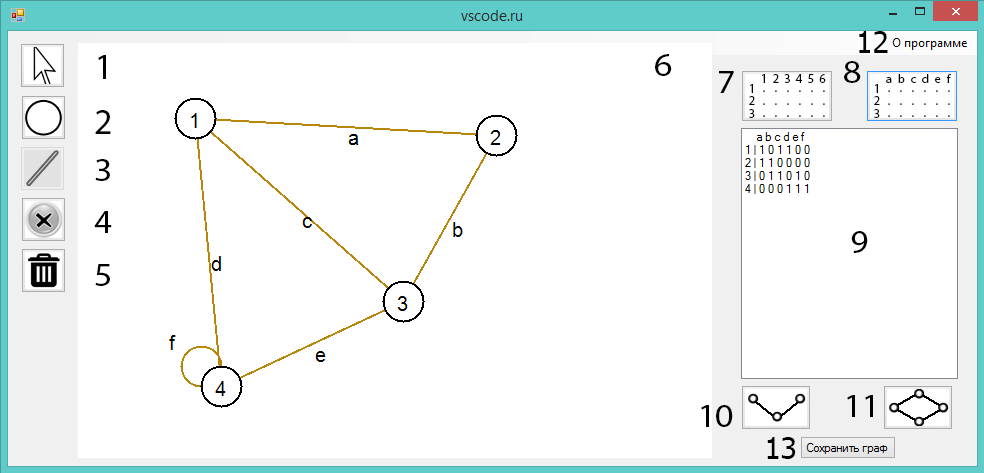
Пользовательский интерфейс программы изображен на рисунке 1. На нем цифрами обозначены элементы управления:
- Выбор вершины (при выборе какой-либо вершины, отображается ее степень).
- Создание вершины.
- Создание ребра.
- Удаление элемента.
- Удаление всего графа.
- Рабочее поле для построения графа.
- Построение матрицы смежности.
- Построение матрицы инцидентности.
- Поле для вывода информации о графе: степень выбранной вершины, матриц смежности и инцидентности, элементарных цепей и циклов.
- Вывод всех элементарных цепей.
- Вывод всех элементарных циклов.
- Информация о программе (окно представлено на рисунке 2).
- Сохранение изображения графа.
Если при построении ребра вы выбрали не ту вершину, то отменить выбор можно, нажав правой кнопкой мыши на выбранной вершине.
Рисунок 2. Окно «О программе»
Описание структуры программы
Опишем ключевые моменты в программном коде.
При кодировании граф был представлен в виде списка (List<>) экземпляров класса Vertex (вершина):
|
1 2 3 4 5 6 7 8 9 10 |
class Vertex { public int x, y; public Vertex(int x, int y) { this.x = x; this.y = y; } } |
где x и y — координаты центра вершины.
И списка (List<>) экземпляров класса Edge (ребро):
|
1 2 3 4 5 6 7 8 9 10 |
class Edge { public int v1, v2; public Edge(int v1, int v2) { this.v1 = v1; this.v2 = v2; } } |
v1 и v2 — номера вершин, которые соединяет ребро.
Вот эти списки:
|
1 2 |
List<Vertex> V; List<Edge> E; |
Когда происходит выбор вершины мышью, поиск нужной вершины из списка осуществляется посредством перебора всех вершин и проверки условия принадлежности точки, в месте щелчка мыши, окружности вершины с помощью уравнения окружности: (x — x0)2 + (y — y0)2 = R2.
|
1 2 3 4 5 6 7 |
for (int i = 0; i < V.Count; i++) { if (Math.Pow((V[i].x - e.X), 2) + Math.Pow((V[i].y - e.Y), 2) <= G.R * G.R) { ... } } |
где e.X, e.Y — координаты точки в месте щелчка мыши, а G.R — радиус окружности вершины.
Заполнение матрицы смежности:
|
1 2 3 4 5 6 7 8 9 10 11 |
public void fillAdjacencyMatrix(int numberV, List<Edge> E, int[,] matrix) { for (int i = 0; i < numberV; i++) for (int j = 0; j < numberV; j++) matrix[i, j] = 0; for (int i = 0; i < E.Count; i++) { matrix[E[i].v1, E[i].v2] = 1; matrix[E[i].v2, E[i].v1] = 1; } } |
numberV — количество вершин в графе. matrix имеет размер [numberV, numberV].
Заполнение матрицы инцидентности:
|
1 2 3 4 5 6 7 8 9 10 11 |
public void fillIncidenceMatrix(int numberV, List<Edge> E, int[,] matrix) { for (int i = 0; i < numberV; i++) for (int j = 0; j < E.Count; j++) matrix[i, j] = 0; for (int i = 0; i < E.Count; i++) { matrix[E[i].v1, i] = 1; matrix[E[i].v2, i] = 1; } } |
где numberV — количество вершин в графе. matrix имеет размер [numberV, E.Count].
Определение степени вершины происходит в результате суммирования элементов строки матрицы смежности с номером, равным номеру выбранной вершины.
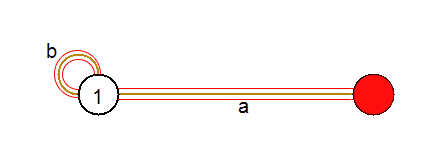
Если нажата кнопка «удаление элемента», то при щелчке мышью на рабочем поле происходит перебор всех элементов графа и поиск элемента, которому принадлежит координата в месте щелчка. При этом для ребер и петель поиск осуществляется с допуском в несколько пикселей, то есть, например, принадлежность точки, в месте щелка, конкретному ребру характеризуется принадлежностью точки области, границами которой выступают прямые, отстоящие вверх и вниз от исходной прямой на несколько пикселей.
Проиллюстрировать вышесказанное можно с помощью рисунка:
Рисунок 3. Области, рассматриваемые при поиске элемента графа для удаления
Красным цветом обозначен тот самый допуск в несколько пикселей при поиске элемента для удаления. Для вершины никакого допуска рассматривать не нужно.
Про поиск элементарных цепей и циклов мы уже рассказывали на vscode.ru. Почитать можно здесь:
Поиск элементарных цепей в графе
Поиск элементарных циклов в графе
Скачать исходник программы, написанной в Visual Studio, можно, нажав на кнопку ниже.
Скачать исходник
Поделиться в соц. сетях: