Рассмотрим алгоритм поиска всех элементарных циклов в неориентированном графе. В этой статье будет приведено описание алгоритма и его реализация на языке программирования C#.
Циклом в графе называется такая конечная цепь, которая начинается и заканчивается в одной вершине. Цикл обозначается последовательностью вершин, которые он содержит, например: (3-5-6-7-3).
Кстати, про цепи, а именно про поиск элементарных цепей в графе мы недавно писали.
Цикл называется элементарным, если все вершины, входящие в него, различны (за исключением начальной и конечной).
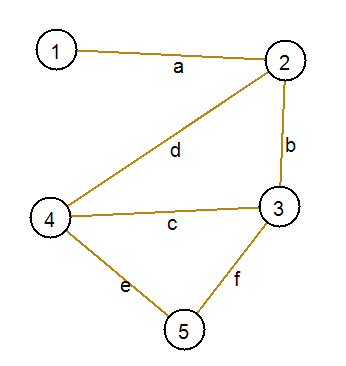
Давайте рассмотрим пример. Пусть дан такой граф:
Перечислим все элементарные циклы в нем: 2-3-4-2, 2-3-5-4-2, 3-2-4-3, 3-2-4-5-3, 3-4-5-3, 4-3-2-4, 4-3-5-4, 4-2-3-5-4, 5-4-3-5, 5-4-2-3-5.
Допустим граф задается, как G = (V, E), где V – множество вершин графа, а E – множество ребер этого графа. Вершины и ребра представим объектами таких классов:
|
1 2 3 4 5 6 7 8 9 10 11 |
//вершина class Vertex { public int x, y; public Vertex(int x, int y) { this.x = x; this.y = y; } } |
, где x, y – координаты центра вершины на плоскости.
|
1 2 3 4 5 6 7 8 9 10 11 |
//ребро class Edge { public int v1, v2; public Edge(int v1, int v2) { this.v1 = v1; this.v2 = v2; } } |
, где v1, v2 – номера вершин, которые соединяет данное ребро.
Важно! Нумерация вершин начинается с нуля!
Множества вершин и ребер графа будем хранить в списках List<>:
|
1 2 |
List<Vertex> V; List<Edge> E; |
Для поиска всех элементарных циклов в неориентированном графе будем использовать модификацию рекурсивного алгоритма “поиск в глубину” (DFS). DFS (Depth-first search) — это один из алгоритмов для обхода графа. Обязательно почитайте про него подробнее здесь.
Модифицируем алгоритм DFS в DFScycle. Прототип функции DFScycle будет таким:
|
1 |
DFScycle(int u, int endV, List<Edge> E, int[] color, int unavailableEdge, List<int> cycle) |
, где u – номер вершины, в которой мы находимся в данный момент, endV – номер конечной вершины цикла, Е – список ребер, color[] – массив, в котором хранятся цвета вершин, unavailableEdge — см. ниже, cycle – список, в который заносится последовательность вершин искомого цикла.
В конечном итоге будем преобразовывать последовательность номеров вершин цикла из списка cycle в строку вида: «2-6-7-2». Хранить всю совокупность элементарных циклов будем в списке строк:
|
1 |
List<string> catalogCycles; |
Рассмотрим работу алгоритма DFScycle. В начальный момент времени все вершины графа окрашены в белый цвет. Необходимо выполнить следующее:
Перебираем все вершины, любая из них может иметь элементарный цикл. На каждой итерации перекрашиваем все вершины в белый цвет (обозначим его 1, а черный цвет будем обозначать 2). Добавляем в список вершин цикла cycle текущую вершину.
Теперь поговорим про параметр unavailableEdge. Вершину, для которой ищем цикл, перекрашивать в черный цвет не будем, иначе программа не сможет в нее вернуться, поскольку эта вершина окажется недоступной. Поэтому введем переменную unavailableEdge, в которую будем передавать номер последнего ребра, по которому осуществлялся переход между вершинами, соответственно это ребро на следующем шаге окажется недоступным для перехода. В действительности это необходимо только на первом уровне рекурсии, чтобы избежать некорректной работы алгоритма и вывода, например, ошибочного результата поиска 1-2-1 при наличии такого графа:
Вызовем процедуру DFScycle(…).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
private void cyclesSearch() { int[] color = new int[V.Count]; for (int i = 0; i < V.Count; i++) { for (int k = 0; k < V.Count; k++) color[k] = 1; List<int> cycle = new List<int>(); //поскольку в C# нумерация элементов начинается с нуля, то для //удобочитаемости результатов поиска в список добавляем номер i + 1 cycle.Add(i + 1); DFScycle(i, i, E, color, -1, cycle); } } |
Процедура DFScycle(int u, int endV, List<Edge> E, int[] color, int unavailableEdge, List<int> cycle).
- ЕСЛИ номер вершины u не равен endV, то мы не достигли конца элементарного цикла, поэтому перекрашиваем вершину u в черный цвет. ИНАЧЕ ЕСЛИ число вершин в списке cycle больше или равно двум – конец цикла достигнут: добавляем цикл cycle в список catalogCycles и выполняем возврат из функции.
- Для всякой вершины w, смежной с вершиной u и окрашенной в белый цвет, рекурсивно выполняем процедуру DFScycle(w, endV, E, color, unavailableE, cycleNEW), предварительно добавив вершину w в список cycleNEW. Возвращаем вершине w белый цвет (возможно через нее проходят другие циклы, поэтому не будем исключать ее из рассмотрения).
Примечание 1. Поскольку алгоритм обходит граф во все стороны, то выходит, что он обходит цикл в обе стороны, в итоге программа находит одинаковые циклы вида: 1-3-4-1, 1-4-3-1. Получаются своеобразные палиндромы. В реализации функции DFScycle присутствует механизм исключения таких палиндромов из списка результатов поиска.
Примечание 2. Поскольку в языке C# списки List передаются по ссылке (а не по значению), то для корректной работы алгоритма необходимо создавать копию списка cycle cycleNEW и передавать ее [копию] в новый вызов функции DFScycle().
Реализация процедуры DFScycle на языке программирования C#:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
private void DFScycle(int u, int endV, List<Edge> E, int[] color, int unavailableEdge, List<int> cycle) { //если u == endV, то эту вершину перекрашивать не нужно, иначе мы в нее не вернемся, а вернуться необходимо if (u != endV) color[u] = 2; else if (cycle.Count >= 2) { cycle.Reverse(); string s = cycle[0].ToString(); for (int i = 1; i < cycle.Count; i++) s += "-" + cycle[i].ToString(); bool flag = false; //есть ли палиндром для этого цикла графа в List<string> catalogCycles? for (int i = 0; i < catalogCycles.Count; i++) if (catalogCycles[i].ToString() == s) { flag = true; break; } if (!flag) { cycle.Reverse(); s = cycle[0].ToString(); for (int i = 1; i < cycle.Count; i++) s += "-" + cycle[i].ToString(); catalogCycles.Add(s); } return; } for (int w = 0; w < E.Count; w++) { if (w == unavailableEdge) continue; if (color[E[w].v2] == 1 && E[w].v1 == u) { List<int> cycleNEW = new List<int>(cycle); cycleNEW.Add(E[w].v2 + 1); DFScycle(E[w].v2, endV, E, color, w, cycleNEW); color[E[w].v2] = 1; } else if (color[E[w].v1] == 1 && E[w].v2 == u) { List<int> cycleNEW = new List<int>(cycle); cycleNEW.Add(E[w].v1 + 1); DFScycle(E[w].v1, endV, E, color, w, cycleNEW); color[E[w].v1] = 1; } } } |
Результатом выполнения этой процедуры поиска элементарных циклов для графа, рассмотренного выше, будет такая последовательность циклов:
Скачать код процедуры DFScycle
Поделиться в соц. сетях:
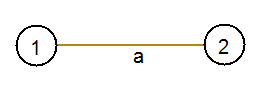

А каким образом мы задаем вершины и ребра ?
Ведь List и List у нас сейчас принимают значение 0
Вершины — в виде списка экземпляров класса Vertex, указывая координаты каждой вершины. Ребра — в виде списка экземпляров класса Edge, указывая для каждого ребра номера вершин, которые оно соединяет.
Подскажите, а как заполнять эти List, желательно примером добавления одной вершины
Создаем List’ы: V = new List (); E = new List ();
List
List
Добавление в List вершины графа:
V.Add(new Vertex(X, Y));
(X, Y) — координаты вершины.
Добавление в другой List ребра:
E.Add(new Edge(n1, n2));
n1, n2 — номера вершин, которые соединяет ребро графа.
Добрый вечер, подскажите, а как переделать алгоритм поиска циклов с использование поиска в ширину? Буду очень благодарен.
Заранее спасибо.
Это довольно сложный вопрос, тема отдельной статьи.
В общем случае:
1) Вам нужно обойти граф с помощью алгоритма поиска в ширину.
2) При обходе записывать маршрут движения по связанным вершинам.
3) Если пришли из вершины в неё же саму, то найден цикл.
Возможны подводные камни в виде нахождения одинаковых маршрутов, соответственно необходим механизм их исключения.
С помощью поиска в ширину никогда обход графа не делал. На мой взгляд для данной задачи (поиска циклов) больше подходит поиск в глубину.
Собрал все куски программы, сделал объявление графа, но когда вызываю функцкию выводит это:
Для нестатического поля, метода или свойства «ConsoleApplication1.Program.cyclesSearch()» требуется ссылка на объект.
Вот кусок кода из мейна..
V.Add(new Vertex(1, 3));
E.Add(new Edge(2, 3));
cyclesSearch();
Пробовал менять статичность/нестатичность но только хуже становилось…
Как это исправить ?
Здравствуйте. Если делать программу в одном файле, то, чтобы всё работало, необходимо поля:
List< string > catalogCycles;
List< Vertex > V;
List< Edge > E;
сделать статическими. Кроме того, нужно создать эти объекты с помощью оператора new.
Методы cyclesSearch и DFScycle — также объявить статическими.
Вот Вам пример, где всё собрано в один файл и работает:
https://yadi.sk/i/8EpLNQLWzjLYv
Конечно, так делать не хорошо. Лучше всего каждый класс помещать в отдельный файл, и сам процесс поиска циклов в графе также выделить в отдельный класс.
Добавил вершины:
V.Add(new Vertex(1, 1));
E.Add(new Edge(1, 2));
V.Add(new Vertex(2, 1));
E.Add(new Edge(3, 4));
V.Add(new Vertex(2, 3));
E.Add(new Edge(4, 5));
V.Add(new Vertex(1, 4));
E.Add(new Edge(3, 4));
V.Add(new Vertex(1, 3));
E.Add(new Edge(2, 3));
После запуска в строке:
if (color[E[w].v2] == 1 && E[w].v1 == u)
(она находиться в DFScycle) вылетает ошибка что u вне границы массива
Дека, нумерация вершин должна начинаться с нуля, а не с единицы.
Не могу понять.. Мы вводим координаты вершины, а не порядок.
Сначала добавляется несколько вершин:
V.Add(new Vertex(10, 40)); //числа — это координаты вершины на плоскости
V.Add(new Vertex(0, 1));
Затем создаются рёбра:
E.Add(new Edge(0, 1)); //тут мы соединили первую вершину со второй
здесь числа — это номера вершин, которые соединяет созданное ребро.
Номера вершин начинаются с нуля. То есть первая вершина в коде является нулевой.
Я бы сказал, что в примере этой статьи не 10, а три цикла. Циклы природно отождествлять, если один из другого получается циклической перестановкой.