В этой статье рассмотрим введение порядковой функции на ориентированном графе. Будет приведено описание алгоритма порядковой функции и его реализация на языке программирования C#.
Описание алгоритма
Начнем с теории. Порядковая функция на ориентированном графе без контуров разбивает множество вершин графа на непересекающиеся подмножества, упорядоченные так, что если вершина входит в подмножество с номером i, то следующая за ней вершина входит в подмножество с номером большим чем i. Полученные непересекающиеся подмножества вершин называются иерархическими уровнями.
Приведем описание алгоритма упорядочения графа:
- В подмножество нулевого уровня N0 включаются все вершины i, в которые нельзя попасть не из какой-либо другой вершины. В этом подмножестве проводится последовательная нумерация вершин 1, 2, …, m.
- В подмножество первого уровня N1 включаются все вершины i, в которые можно попасть только из вершин уровня N0. Проводится нумерация вершин m + 1, m + 2, …, m + r.
- В подмножество N2 включаются все вершины i, в которые можно попасть только из вершин более низких уровней и т.д. Подобная процедура продолжается до тех пор, пока не будут пронумерованы все вершины графа.
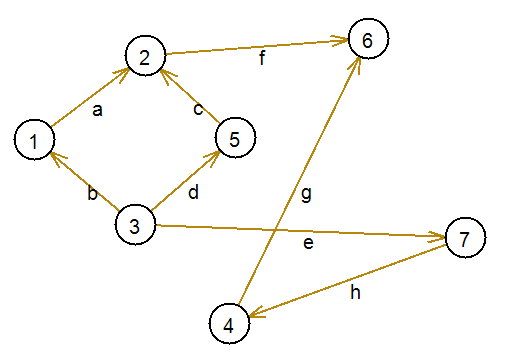
Рассмотрим пример. Пусть имеется граф, как на рисунке ниже.
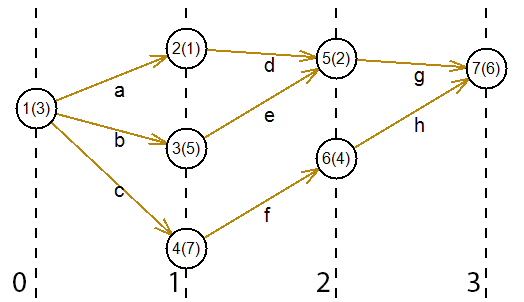
После введения порядковой функции на этом графе, получим следующее:
Реализация алгоритма
Рассмотрим реализацию алгоритма введения порядковой функции на графе. Для разработки будет использоваться язык C#.
Пусть дуга графа представляет собой экземпляр класса Edge:
|
1 2 3 4 5 6 7 8 9 10 |
public class Edge { public int v1, v2; public Edge(int v1, int v2) { this.v1 = v1; this.v2 = v2; } } |
, где v1 — номер вершины, из которой дуга исходит, а v2 — номер вершины, в которую данная дуга заходит.
Иерархический уровень упорядоченного графа представим экземпляром класса HierarchicalLevel:
|
1 2 3 4 5 6 7 8 9 |
public class HierarchicalLevel { public List<int> level; public HierarchicalLevel() { level = new List<int>(); } } |
, где level — список номеров вершин, входящих в данный иерархический уровень.
Всё множество дуг и иерархических уровней упорядоченного графа будем хранить в виде соответствующих списков:
|
1 2 |
List<Edge> E; List<HierarchicalLevel> HL = new List<HierarchicalLevel>(); |
Приведем реализацию метода createHLevel(…), упорядочивающего граф.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
public void createHLevel(List<HierarchicalLevel> HL, int numberV, List<Edge> E) //numberV - количество вершин { List<int> usedV = new List<int>(); //список вершин, уже использованных в порядковой функции List<int> notUsedV = new List<int>(); //список вершин, еще не использованных в порядковой функции for (int i = 0; i < numberV; i++) notUsedV.Add(i); while (notUsedV.Count > 0) { HL.Add(new HierarchicalLevel()); for (int i = 0; i < notUsedV.Count; i++) { int k = 0; for (int j = 0; j < E.Count; j++) if (E[j].v2 == notUsedV[i]) k++; //считаем полустепень захода вершины for (int m = 0; m < usedV.Count; m++) for (int j = 0; j < E.Count; j++) { if (E[j].v1 == usedV[m] && E[j].v2 == notUsedV[i]) k--; //вычитаем дуги, иходящие из вершин предыдущих уровней и входящие в вершину i } if (k == 0) { HL[HL.Count - 1].level.Add(notUsedV[i]); notUsedV.RemoveAt(i); i--; } } for (int j = 0; j < HL[HL.Count - 1].level.Count; j++) { usedV.Add(HL[HL.Count - 1].level[j]); } } } |
Аргументы метода createHLevel: HL — список иерархических уровней графа, numberV — количество вершин в графе, E — список дуг в графе.
Кратко опишем принцип работы метода createHLevel(). В начале все вершины считаются неиспользованными и заносятся в список notUsedV. Программа продолжает работу, пока список notUsedV не окажется пустым. На каждой итерации для данного иерархического уровня перебираются все вершины из списка notUsedV. Для каждой вершины из этого списка вычисляется ее полустепень захода (int k), затем из этого числа вычитается количество дуг, входящих в вершину из вершин предыдущих уровней (эти вершины хранятся в списке usedV). Если в итоге k оказывается равным нулю, значит вершина принадлежит данному уровню: добавляем ее список вершин уровня и удаляем из списка неиспользованных вершин. В конце итерации для данного иерархического уровня обновляем список использованных вершин usedV: добавляем в него номера вершин, занесенных в данный уровень.
Если вы хотите скачать код метода createHLevel, то нажмите на кнопку ниже.
Скачать код метода createHLevel
Примечание
Поскольку введение порядковой функции возможно только на графе без контуров, то можно сделать соответствующую проверку графа на их наличие. На нашем сайте мы рассматривали алгоритм поиска циклов в неориентированном графе, немного модифицировав его, а именно, убрав обратный проход по ребру, вы получите функцию для поиска контуров в ориентированном графе.
Поделиться в соц. сетях: