Не так давно мы разбирали сортировку методом пузырька на языке C#. Теперь давайте рассмотрим сортировку выборкой.
Описание алгоритма:
На первом шаге в массиве находится элемент с минимальным значением, затем он меняется местами с элементом, находящемся на нулевой позиции массива(если минимальный элемент и так находится на нулевой позиции, обмен, соответственно, не производится), и затем выбывает из процесса сортировки. В следующей итерации среди оставшихся чисел находится второй по минимальности элемент, и происходит обмен местами этого элемента с элементом на первой позиции массива и тоже выбывает. Затем ищется третий по минимальности элемент, меняется позициями с третьим элементом в массиве и выбывает из сортировки, и так далее. После всех итерации получится отсортированный от минимального к максимальному значению массив.
Пример:
Сортировка методом выбора проходит следующим образом.
К примеру, у нас имеется массив 3 9 1 4 0
Проводим первую итерацию. Ищем минимальный элемент массива. Для этого берём число на первой позиции, условно обозначаем его как минимальное и сравниваем с остальными. Если найдётся число, которое окажется меньше, чем нынешнее, то такое число обозначается минимальным, а затем также сравнивается с последующими. Таким образом, после прохода по всему массиву, мы найдём элемент с самым маленьким числовым значением.
Затем мы меняем местами найденное минимальное число с элементом на нулевой позиции в массиве и «выкидываем» эту нулевую позицию из процесса сортировки.
Жирным шрифтом будет обозначаться нынешний минимальный элемент.
3 9 1 4 0
Нынешний минимальный элемент сравнивается с 9. Он меньше, чем 9, поэтому сравнивается со следующим элементом. 1 меньше, чем 3, следовательно, теперь 1 — это наш нынешний минимальный элемент.
3 9 1 4 0
Продолжаем сравнение. 1 меньше 4, но 0 меньше 1, значит теперь он считается минимальным элементом.
3 9 1 4 0
Мы прошли по массиву и нашли самый маленький его элемент.
Теперь мы меняем местами этот элемент с элементом на нулевой позиции и больше не сравниваем его ни с чем (так как это бессмысленно и только занимает лишнее время), уменьшая количество шагов в итерации на 1.
0 9 1 4 3
Вторая итерация. Принимаем первый элемент среди оставшихся неупорядоченных чисел за минимальный и сравниваем его с остальными.
0 9 1 4 3
Единица меньше 9, теперь она минимальная.
0 9 1 4 3
Единица сравнивается с 4 и с 3, но все эти числа больше неё, следовательно, это и есть наш следующий минимальный элемент.
Мы меняем его местами с элементом на первой позиции массива и опять сокращаем количество шагов в итерации на 1.
0 1 9 4 3
Третья итерация. Таким же образом ищем следующее минимальное число.
0 1 9 4 3
Четвёрка меньше девятки.
0 1 9 4 3
Тройка меньше четвёрки. Мы обошли весь массив, значит 3 и является минимальными значением. Меняем его местами с элементном на второй позиции массива.
0 1 3 4 9
Четвёртая итерация. Сравниваем оставшиеся числа. Нынешнее минимальное число 4 меньше, чем 9, значит оно остаётся на своём месте, а так как у нас после него остаётся последнее число 9 в массиве, то оно, соответственно, является максимальным из всего массива. Сортировка окончена.
Таким образом у нас получается упорядоченный методом выбора массив:
0 1 3 4 9
Код программы:
В программе для начала создаём функцию сортировки.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
static int[] ViborSort(int[] mas) { for (int i = 0; i < mas.Length - 1; i++) { //поиск минимального числа int min=i; for (int j = i + 1; j < mas.Length; j++) { if (mas[j] < mas[min]) { min = j; } } //обмен элементов int temp = mas[min]; mas[min] = mas[i]; mas[i] = temp; } return mas; } |
В строках 7-14 мы ищем минимальный элемент массива. Происходит это так же, как описано в примере.
В строках 16-18 мы меняем местами элементы. В переменную temp записываем минимальный элемент массива. Затем на позицию минимального элемента записываем элемент, на чьё место он должен встать (на первой итерации — нулевая позиция, на второй итерации — первая, и так далее; это контролируется условием в строке 4), а затем, на эту самую позицию, которую мы освободили, вставляем значение из переменной temp.
В главную функцию main мы вернём уже упорядоченный массив (строка 20).
Теперь рассмотрим, что у нас будет в функции main.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
static void Main(string[] args) { Console.WriteLine("Ведите количество чисел для сортировки."); int N = Convert.ToInt32(Console.ReadLine()); Console.WriteLine("Введите числа для сортировки:"); int[] mas = new int[N]; for (int i = 0; i < mas.Length; i++) { mas[i] = Convert.ToInt32(Console.ReadLine()); } ViborSort(mas); Console.WriteLine("Отсортированный массив:"); for (int i = 0; i < mas.Length; i++) { Console.WriteLine( mas[i]); } Console.ReadLine(); } |
В строках 3-10 мы просим пользователя ввести количество элементов массива и сами эти значения, и считываем их.
Затем вызываем функцию ViborSort(mas), куда передаём заполненный массив. Там он упорядочивается и возвращается. Нам остаётся только вывести его в в консоль, что мы и делаем в строках 12-17.
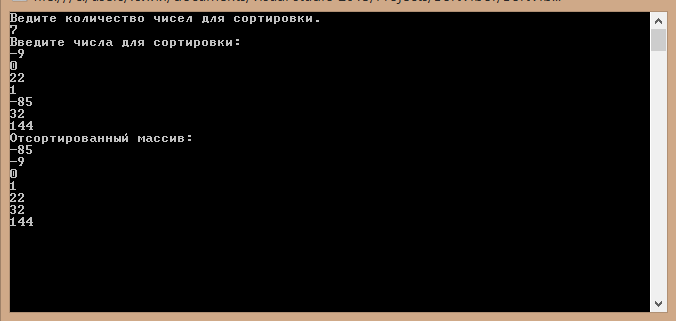
В консоли наша сортировка методом выбора будет выглядеть вот так:
Скачать программу «Сортировка методом выбора на C#» можно ниже:
Скачать исходник
Поделиться в соц. сетях:
Здравствуйте. Можно ли утверждать, что сортировка методом выбора эффективнее, чем пузырьковая, рассмотренная ранее? — если можно, поясните почему, пожалуйста. :)
Оба алгоритма имеют одинаковую вычислительную сложность (n * n). Единственный плюс сортировки пузырьком в том, что если массив уже отсортирован, то потребуется всего один проход функции для завершения работы алгоритма, а в случае с сортировкой методом выбора все равно будет произведено n * n операций.